Матрично-структурные модели для имитации динамического поведения ЭМС

Как было отмечено ранее, имитационный эксперимент, подготовленный в целях анализа динамического поведения системы, может выполняться в комбинированном компилирующе-интерпретирующем или компилирующем режимах работы. В соответствии с этим можно выделить два вида МСМ, а именно:

• дифференциальная матрично-структурная модель (ДМСМ),
• алгебраическая матрично-структурная модель (АМСМ).

В совокупность данных ДМСМ кроме значений параметров, характеристик элементов и координат модели включаются производные последних. Параметры АМСМ вместо производных координат модели содержат их значения в дискретные моменты времени.

В свою очередь каждый вид МСМ подразделяется на две формы. Так ДМСМ может быть представлена как структурная матрица, соответствующая детализированному графу системы или как матрица дифференциальных и алгебраических уравнений, записанных в форме Коши. Для линейной непрерывной модели объекта первая форма дифференциальной матрично-структурной модели - ДМСМ_1 соответствует детализированной структурной матрице, а вторая форма ДМСМ_2 - векторно-матричной модели.

Таким образом, для изучения динамического поведения методом имитационных экспериментов системы, идентифицированной с помощью ДМСМ_2 необходимо выполнить численное интегрирование уравнений, записанных в каждой строке матрицы моделей.

При представлении системы с помощью ДМСМ_1 требуется предварительная сортировка уравнений матрицы, что соответствует преобразованию модели к ДМСМ_2.

Матрица первой формы алгебраической матрично-структурной модели АМСМ_1 соответствует детализированному графу системы, в котором непрерывные интеграторы заменены их дискретными аналогами в соответствии с выбранным методом численного интегрирования. Матрица второй формы алгебраической матрично-структурной модели АМСМ_2 соответствует дереву вычислений, полученному после преобразования АМСМ_1. АМСМ_2 используется для выполнения имитационного эксперимента, который сводится к последовательному вычислению алгебраических выражений, записанных в строках матрицы модели.

Таким образом, АМСМ_1 представляет собой матричную запись замкнутой алгебраической имитационной модели (АИМ) системы, а АМСМ_2 - разомкнутой АИМ.

Формирование матрично-структурной модели для комбинированного режима имитационного эксперимента

Исходной информацией для формирования матрично-структурной модели здесь является матричное отображение структурной модели математического уровня (СММУ). В общем случае СММУ представляет собой схему соединения динамических элементов, обеспечивающих свойства L- N- ND- NVS- моделей.

СММУ является в большинстве случаев результатом преобразования СМФУ, но может также вводиться пользователем.

СММУ, введенная пользователем, содержит линейные инерционные элементы, представленные произвольным видом передаточной функции. Поэтому для получения ДМСМ_1 необходимо выполнение отдельных операций преобразования.

Процесс преобразования СММУ в ДМСМ_1 сводится к декомпозиции линейных инерционных элементов на интеграторы и безынерционные звенья. Для алгоритмизации этой операции применяется универсальный метод разложения произвольной передаточной функции на n дифференциальных уравнений первого порядка и одно алгебраическое выражение (Метод Вульфсона [2]).

Элементы, обеспечивающие специфические свойства N-, ND-, и NVS-моделей, идентифицируются в ДМСМ списком:

(6.1)

который включает в себя идентификатор класса (N, D, C, K, DA, Z, ...[1]), имя функционального элемента, значения параметров.

Формально ДМСМ_1 представляется также в виде матрицы

(6.2)

включающей в себя два блока: квадратную матрицу взаимосвязей и параметров P и прямоугольную матрицу входных воздействий V.

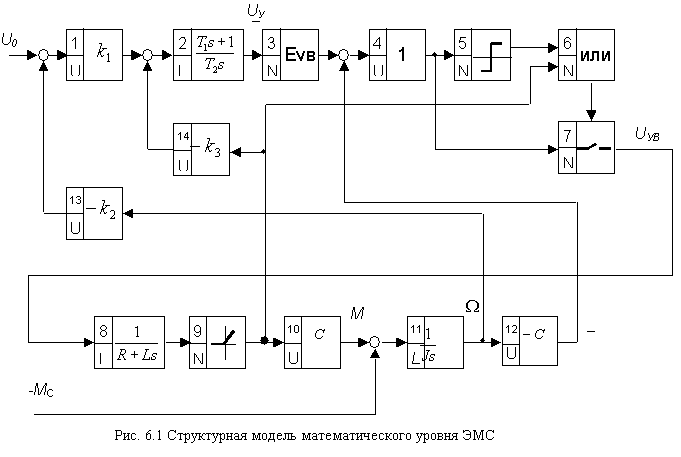
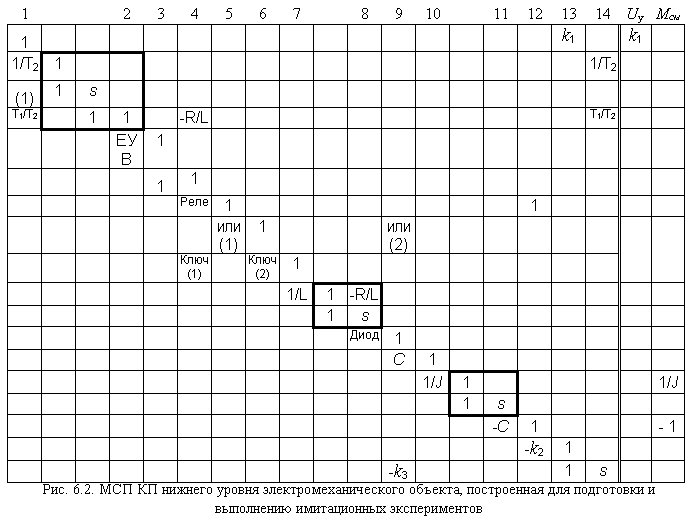
На рис. 6.1 в качестве примера приведены СММУ электропривода постоянного тока с нереверсивным тиристорным управляемым выпрямителем [4], построенная и введенная пользователем. Матрично-структурное представление этой модели в форме ДМСМ_1. Представлено на рис. 6.2.

Анализ содержания рис. 6.1 - рис. 6.2. позволяет сформулировать алгоритм формирования ДМСМ_1, включающий в себя два этапа:

1. Согласно алгоритму построения структурных матриц для систем управления, изложенному в лекции 4, записывается матрично-структурное представление СММУ. При этом элементы, обеспечивающие специфические свойства N-, ND-, и NVS-моделей, рассматриваются как безынерционные звенья, коэффициенты передачи соответствуют списку (6.1).
Выполняется детализация МСП в соответствии с алгоритмом формирования детализированных структурных матриц.

Очевидно, что ДМСМ_1 непригодна для отправки на "переработку" процедурам численного интегрирования дифференциальных уравнений. Для получения корректных результатов имитационного эксперимента, уравнения, полученные непосредственно из строк матрицы ДМСМ_1, необходимо пересортировать в соответствии направлениями прохождения сигналов.

Это объясняется последовательным характером вычислений, выполняемых компьютером. Выполнение указанной операции приводит к формированию ДМСМ_2.

Процесс преобразования ДМСМ_1 к ДМСМ_2 очень близок по своей сути к процессу конструирования векторно-матричных моделей.

Непосредственное преобразование N-, ND-, и NVS-моделей в векторно-матричную модель не возможно, так как элементы, обеспечивающие специфические свойства N-, ND-, и NVS-моделей, нельзя идентифицировать неизменным значением коэффициента передачи KN. В этом случае с помощью второго этапа алгоритма конструирования ВММ формируется в табличном виде план вычислительного процесса, который и представляет собой ДМСМ_2.

Первоначально рассмотрим ход построения ДМСМ_2 на упрощенном примере, приведенном на рис. 6.3.

После исключения из детализированного графа ветвей с интеграторами выходы интеграторов становятся внешними входными воздействиями. Численные значения этих воздействий определяются значениями выходов соответствующих интеграторов на предыдущем шаге. Как правило, после выполнения указанной операции детализированный граф преобразуется в дерево вычислений. Если же после исключения интеграторов остаются замкнутые безынерционные контуры, следует принять меры для их исключения:

• преобразовать исходную структурную модель системы;
• воспользоваться средствами построения СММУ на языке математических уравнений, где предусмотрено численное решение алгебраических уравнений;
• использовать АМСМ, которые обеспечивают развязку безынерционных контуров.

Граф-модель дерева вычислений, полученного для нашего упрощенного примера и соответствующая ему ДМСМ_2 приведены на рис. 6.4.

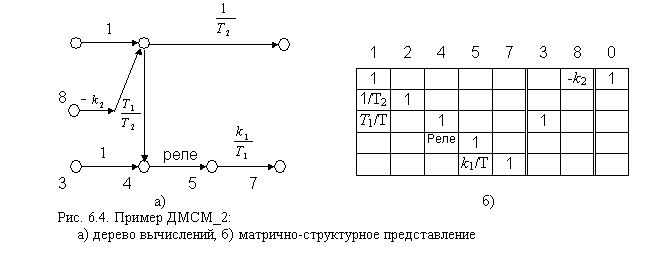
Сравнительный анализ обеих форм дифференциальных матрично-структурных моделей (ДМСМ_1 ДМСМ_2) позволяет определить основные этапы алгоритма конструирования ДМСМ_2.

1. Выполнение M₁-преобразование ДМСМ_1, представленной матрицей S_D1, для которого необходимо
   • идентифицировать в подматрице строки производных и столбцы переменных состояния;
   • столбцы переменных состояния переместить вправо за подматрицу ;
   • из полученной матрицы удалить строки производных.

   В результате этого преобразования получается матрица вычислительной модели

   

   (6.3)

   которая включает в себя квадратную подматрицу размером , прямоугольную подматрицу внешних воздействий размером и прямоугольную подматрицу или вектор размером . Здесь и .

2. Определение списка номеров Z ={z1, z2, ... ,zq2} строк матрицы S_D2, указывающего очередность обработки уравнений, записанных в этих строках, которое заключается
   • в идентификации n строк матрицы S_D2, соответствующих производным переменных состояния, и записи их номеров в конец списка Z на позиции c q₂-n+1 по q₂;
   • в последовательном заполнении освободившихся позиций списка номерами ближайших строк.
3. На основании информации, содержащейся в матрице S_D2 и списке Z, формирование уравнений для дальнейшего использования их процедурами численного интегрирования.

   Формально указанный алгоритм сводится к перестановке строк матрицы S_D2, согласно списку Z, и стандартным вычислениям диагональных элементов модифицированной матрицы.

   При использовании в качестве исходной информации концептуальной модели, построенной из типовых функциональных блоков, эффективность процесса конструирования ДМСМ_2 может быть также повышена за счет изменения общей схемы выполнения преобразований.

   Если M₁ - преобразование выполнить для каждого функционального блока и использовать полученные результаты для формирования ДМСМ_2, то уменьшится объем преобразуемой информации и снизятся затраты на преобразования.

   В большинстве случаев результаты M₁ - преобразования для типовых функциональных блоков целесообразно хранить базе моделей. В этом случае из процесса преобразования исключается этап формирования ДМСМ_1.

продолжение...