Лекция 9

Логарифмические частотные характеристики динамических звеньев

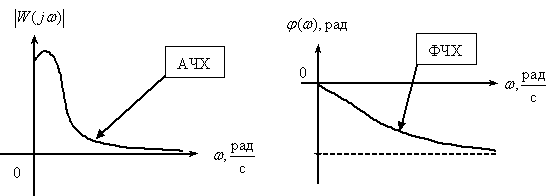
При рассмотрении и сравнение частотных характеристик амплитудных и фазочастотных для устройств различных видов возникает проблема их компактного представления, так как значения амплитуд и частот (см. рис. 1) существенно различаются друг от друга. Кроме того, и сама величина диапазона частот, в котором характеристики конкретного устройства представляют интерес, может быть весьма значительна, от долей герц до десятков мегагерц.

Рис. 1

Решение этой проблемы лежит в использовании логарифмических масштабов в частотных характеристиках.

Впервые обратились к логарифмическим масштабам в технике связи, так как там рассматриваются объекты, как с большими коэффициентами усиления, так и объекты которые характеризуются существенным затуханием сигналов.

В технике связи используют понятие коэффициента передачи по мощности для четырехполюсника, показанного на рис. 2,

Рис. 2

.

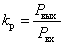Значительный диапазон изменения этого коэффициента и заставил использовать логарифмическое представление, логарифмический коэффициент передачи по мощности –

Логарифмический коэффициент усиления по мощности измеряют специальными единицами, которые носят название Белл (Б).

1 Белл соответствует усилению мощности в 10 раз.

Чаще используют единицу в десять раз меньшую – децибел (дБ).

.

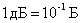При определении логарифмического коэффициента в децибелах, выражение (1) принимает вид –

.

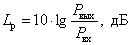Логарифмический коэффициент усиления можно выразить через отношение выходного и входного напряжений при одинаковых нагрузочных сопротивлениях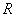

.

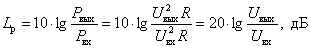Такое представление коэффициента усиления используют в теории автоматического управления для измерения амплитуды частотной характеристики в децибелах –

По оси частот в теории автоматического управления так же используют логарифмический масштаб на основе десятичного логарифма частоты.

При этом ось частот будет иметь следующий вид –

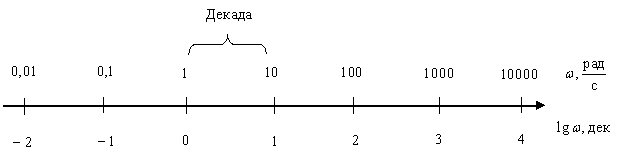
Рис. 3

Изменение частоты в десять раз называют декадой. Причем на оси частот, при ее логарифмическом масштабе, принято обозначать значения частоты в рад/с, иногда в герцах, особенно это принято в радиотехнике и в инженерной практике.

Особо отметим, что логарифмическая шкала не имеет нуля и может пересекаться вертикальной осью в любом месте, что особенно важно тем, что дает возможность рассматривать частотные свойства динамических звеньев и конкретных устройств в необходимом диапазоне изменения частот, где характеристика представляет интерес для исследователя.

Теперь дадим определение логарифмическим частотным характеристикам.

Логарифмической амплитудной частотной характеристикой (ЛАЧХ) динамического звена называют такое представление амплитудной частотной характеристики (АЧХ), в котором модуль (амплитуда) частотной характеристики выражен в децибелах, а частота – в логарифмическом масштабе.

Логарифмической фазовой частотной характеристикой (ЛФЧХ) динамического звена называют такое представление фазочастотной характеристики (ФЧХ) , в котором частота выражена в логарифмическом масштабе.

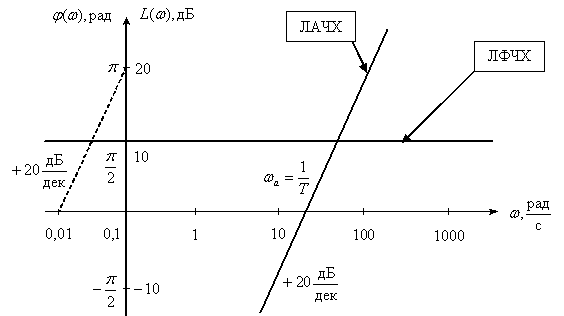
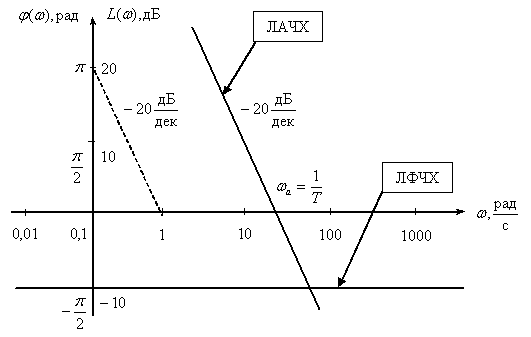
Довольно часто ЛАЧХ И ЛФЧХ строятся на одном графике, чтобы давать полное представление о свойствах объекта, покажем на рис. 4 примерный вид и оформление ЛАЧХ и ЛФЧХ некоторого инерционного объекта.

Логарифмические частотные характеристики элементарных динамических звеньев

Безынерционное звено

Передаточная функция –

.

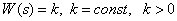Частотная характеристика –

,

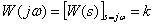АЧХ и ФЧХ

.

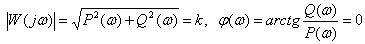Логарифмические характеристики

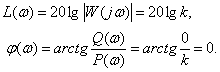
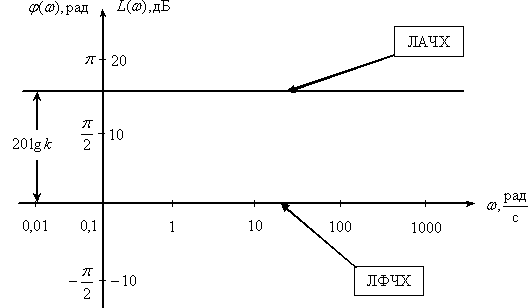
Дифференцирующее звено

Передаточная функция –

.

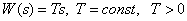Частотная характеристика –

,

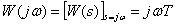АЧХ и ФЧХ

.

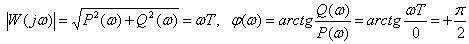Логарифмические характеристики

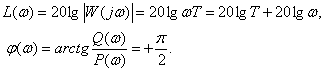
Для удобства построения определим точку, где ЛАЧХ пересекает ось частот –

.

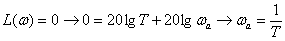Определим наклон ЛАЧХ

,

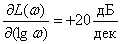то есть, получаем, что ЛАЧХ получает приращение 20 децибел на интервале частот в 1 декаду.

Интегрирующее звено

Передаточная функция –

.

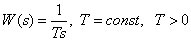Частотная характеристика –

,

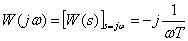АЧХ и ФЧХ

.

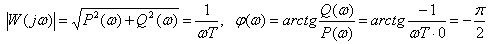Логарифмические характеристики

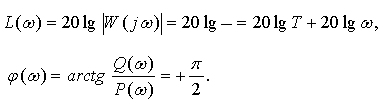
Для удобства построения определим точку, где ЛАЧХ пересекает ось частот –

.

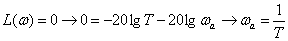Определим наклон ЛАЧХ

,

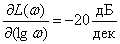то есть, получаем, что ЛАЧХ получает уменьшение на 20 децибел на интервале частот в 1 декаду.

Контрольные вопросы и задачи

1. Дайте определение величине в 1 Белл.

2. Каким образом вычисляется логарифмический коэффициент усиления по мощности для четырехполюсников?

3. Что определяет понятие "декада" применительно к логарифмическим частотным характеристикам?

4. Дайте определение логарифмической амплитудной частотной характеристике.

5. Дайте определение логарифмической амплитудной частотной характеристике.

6. Перечислите основные достоинства логарифмических частотных характеристик по сравнению с обычными частотными характеристиками.

7. Передаточная функция звена –

,

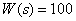как зависит от частоты ЛАЧХ этого звена? Определите ЛАЧХ этого звена.

Ответ:

ЛАЧХ не зависит от частоты,

.

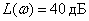8. Передаточная функция звена –

,

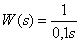определите значение ЛАЧХ этого звена при частоте .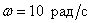

Ответ:

.

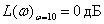9. Передаточная функция звена –

,

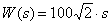определите наклон ЛАЧХ этого звена.

Ответ:

Наклон ЛАЧХ этого звена составляет 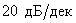.