Лекция 8
Ориентированные графы систем автоматического управления
Математическую модель САУ можно наглядно представить с помощью ориентированных графов (орграфов).
Орграфы используются в сложных САУ, особенно при управлении и автоматизации технологических процессов в промышленности, когда описание в виде структурных схем становится громоздким и сложным для восприятия. Рассмотрим простейший орграф динамического звена САУ.

Рис. 1
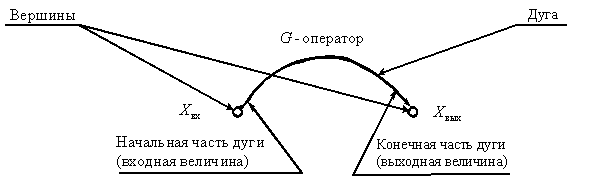
Орграфом САУ является графическое представление САУ в виде совокупности вершин, соответствующих переменным, и дуг, соединяющих вершины.
Рассмотрим основные свойства орграфа:
Каждая дуга со стрелкой, указывающей направление распространения сигнала, изображает звено и характеризуется оператором изображаемого звена (передаточной функцией);
Каждой вершине, отмеченной кружком, ставится в соответствие одна из переменных САУ (изображение переменной по Лапласу);
Входная величина дуги равна переменной вершины, из которой эта дуга исходит;
Выходная величина дуги получается как результат преобразования оператором входной величины;
Если к вершине подходят несколько дуг, то соответствующая вершине переменная равна сумме выходных величин этих дуг (аналог суммирующего звена структурных схем);
Если из вершины исходит несколько дуг, то входные величины всех этих дуг одинаковы (аналог точки ветвления в структурных схемах).
Ориентированный граф (орграф) можно построить по структурной схеме и наоборот. При построении орграфа по структурной схеме необходимо придерживаться следующих правил:
Модифицируют структурную схему так, чтобы в сумматорах все переменные складывались с положительным знаком, отрицательные знаки вносятся в передаточные функции соответствующих звеньев;
Каждый сумматор структурной схемы заменяется вершиной, которой ставится в соответствие выходная переменная сумматора;
Каждое динамическое звено заменяется дугой с оператором, равным передаточной функции звена;
Каждой переменной, включая и входные воздействия, соответствует своя вершина.
Рассмотрим пример. На рис. 2 показана структурная исходная схема, на рис. 3 показан полученный орграф САУ.
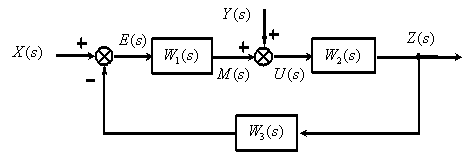
Рис. 2
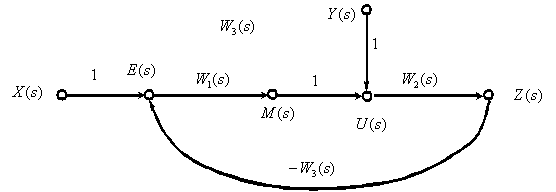
Рис. 3
Преобразовать орграф САУ можно, как и структурную схему, используя правила эквивалентных преобразований для орграфов, которые легко могут быть получены по аналогичным правилам для структурных схем.
Последовательное соединение динамических звеньев.

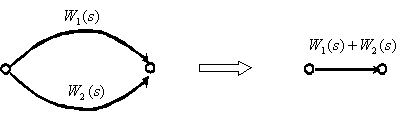
Параллельное соединение динамических звеньев.
Замкнутый контур с отрицательной обратной связью.
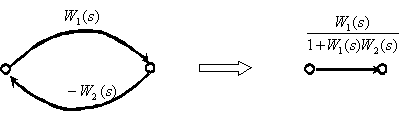
Замкнутый контур с положительной обратной связью.
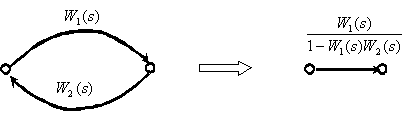
Перенос точки ветвления через динамическое звено.
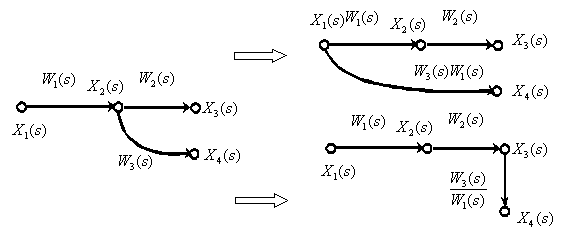
Перенос суммирующего звена через динамическое звено.
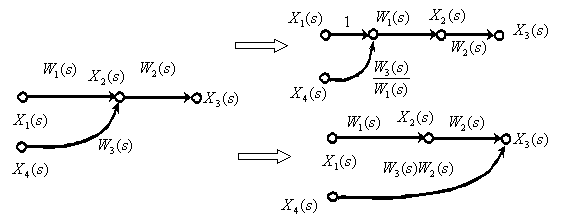
Использование формулы Мейсона для преобразования структурных схем и ориентированных графов
Когда структурная схема преобразована в орграф, для нахождения необходимой передаточной функции можно использовать формулу Мейсона (правило некасающихся контуров), которая позволяет получить передаточную функцию, связывающую переменные в сложных, многоконтурных САУ.
Рассмотрим общий вид формулы и поясним ее компоненты:
|
|
(1) |
где 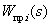 - передаточная функция
- передаточная функция 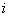 -го отдельного прямого пути от
-го отдельного прямого пути от 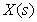 до
до 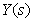 , вычисленная как произведение передаточных функций дуг, входящих в этот путь;
, вычисленная как произведение передаточных функций дуг, входящих в этот путь;
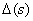 - определитель орграфа.
- определитель орграфа.
|
|
(2) |
где 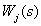 - передаточная функция
- передаточная функция 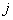 -го замкнутого контура, вычисленная как произведение передаточных функций дуг, входящих в этот контур;
-го замкнутого контура, вычисленная как произведение передаточных функций дуг, входящих в этот контур;
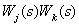 - произведение передаточных функций пары (
- произведение передаточных функций пары (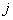 -го и
-го и 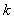 -го) замкнутых контуров, не касающихся ни дугами, ни вершинами, суммирование осуществляется по всем парам некасающихся контуров;
-го) замкнутых контуров, не касающихся ни дугами, ни вершинами, суммирование осуществляется по всем парам некасающихся контуров;
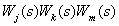 - произведение тройки (
- произведение тройки (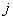 -го,
-го, 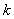 -го и
-го и 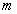 -го) некасающихся контуров, суммирование производится по всем тройкам не касающихся контуров.
-го) некасающихся контуров, суммирование производится по всем тройкам не касающихся контуров.
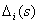 - определитель орграфа, полученного при удалении дуг и вершин
- определитель орграфа, полученного при удалении дуг и вершин 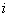 -го отдельного прямого пути, определяется по формуле (2).
-го отдельного прямого пути, определяется по формуле (2).
Поясним использование формулы Мейсона.
В начале выявляются все отдельные прямые пути между входной и выходной переменными, для которых необходимо определить передаточную функцию. Отдельным прямым путем считается такая последовательность дуг и вершин, которая соединяет вершины, соответствующие входному и выходному сигналам. При этом отдельный прямой путь не должен пересекать в вершинах сам себя.
Далее выявляются все замкнутые контуры в орграфе САУ. Замкнутым считается такой контур, когда между двумя вершинами имеется как прямая, так и обратная связь. Передаточная функция замкнутого контура определяется как произведение передаточных функций всех дуг, входящих в контур с учетом знаков.
После того как выявлены все замкнутые контуры орграфа, необходимо проанализировать – есть ли контуры, которые не касаются ни дугами, ни вершинами, есть ли пары, тройки и т. д. таких контуров.
На основании полученного формируется определитель орграфа по формуле (2).
Определители орграфов, полученных после изъятия 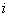 -х отдельных прямых путей, также формируются по формуле (2), при этом учитываются только те контуры, которые остаются после изъятия
-х отдельных прямых путей, также формируются по формуле (2), при этом учитываются только те контуры, которые остаются после изъятия 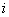 -го прямого пути. Если после изъятия прямого пути не остается ни одного замкнутого контура, определитель такого орграфа принимается равным единице.
-го прямого пути. Если после изъятия прямого пути не остается ни одного замкнутого контура, определитель такого орграфа принимается равным единице.
В качестве примера определим передаточную функцию между 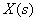 и
и 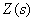 в структурной схеме САУ, показанной на рис. 4, полагая в соответствии с принципом суперпозиции
в структурной схеме САУ, показанной на рис. 4, полагая в соответствии с принципом суперпозиции 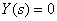 .
.
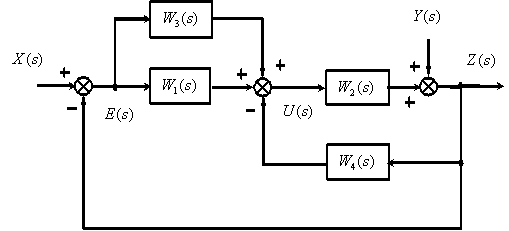
Рис. 4
Преобразуем структурную схему в ориентированный граф (рис. 5).
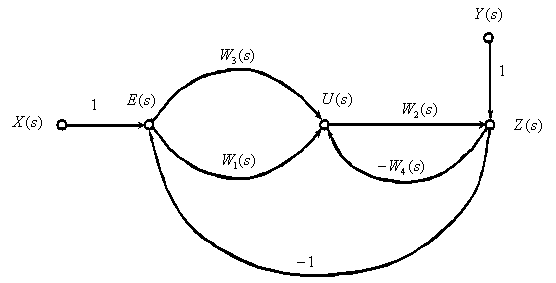
Рис. 5
Определим прямые пути:
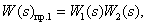
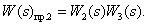
Определим замкнутые контуры:
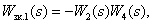
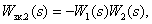
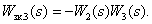
Все контуры имеют общую дугу 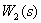 , поэтому некасающихся контуров нет. Определитель орграфа имеет вид
, поэтому некасающихся контуров нет. Определитель орграфа имеет вид
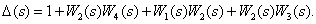
При изъятии 1-го или 2-го прямых путей в орграфе не сохраняется ни одного замкнутого контура, поэтому
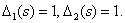
Передаточная функция имеет вид
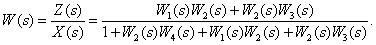
Контрольные вопросы и задачи
Дайте определение орграфа динамического звена.
Поясните процедуру преобразования структурной схемы САУ в ориентированный граф.
Что называется отдельным прямым путем при использовании правила некасающихся контуров?
Какие замкнутые контуры называют некасающимися?
Определите передаточную функцию
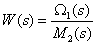
по следующей структурной схеме
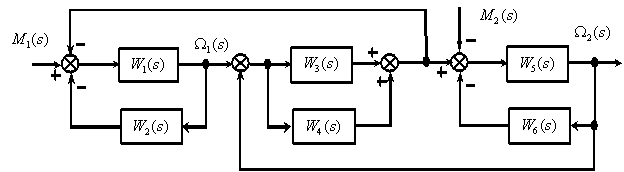
Ответ:
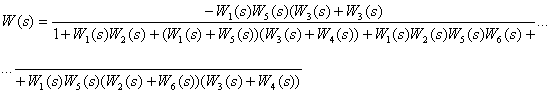 .
.
Определите передаточную функцию
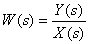
по следующей структурной схеме
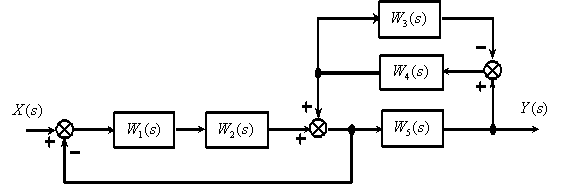
Ответ:
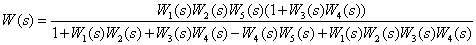 .
.
Определите передаточную функцию
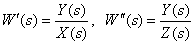
по следующей структурной схеме
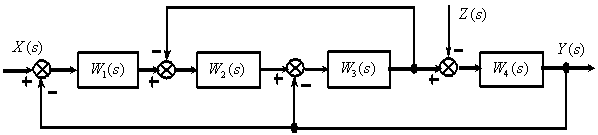
Ответ:
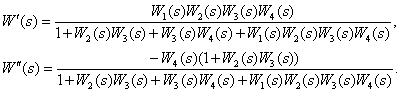 .
.
Определите передаточную функцию
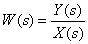
по следующей структурной схеме
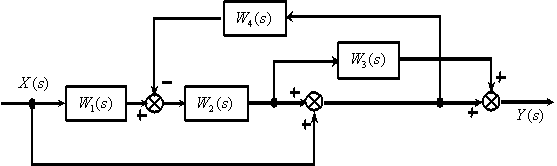
Ответ:
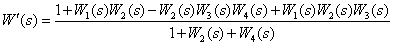 .
.