Лекция 6

Временные и частотные характеристики звеньев

Апериодическое звено

Передаточная функция

.

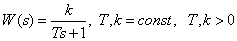Временные характеристики

,

.

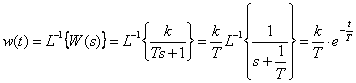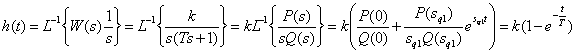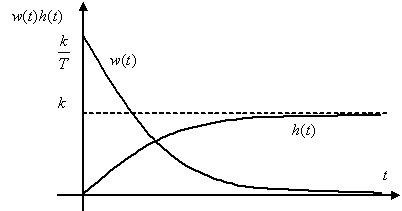
Частотная характеристика

,

.

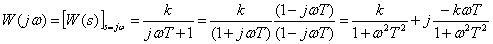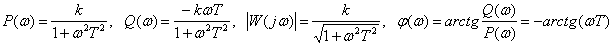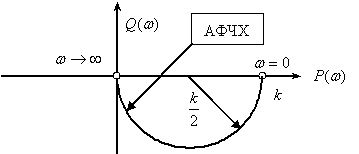
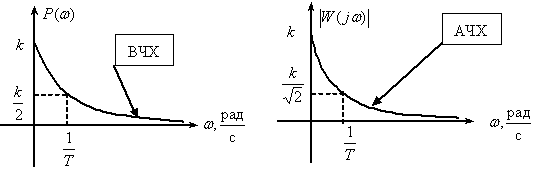
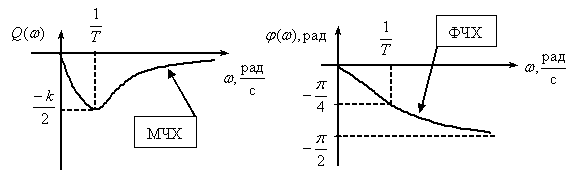
Реальное дифференцирующее звено

Передаточная функция

.

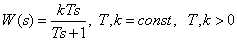Преобразуем передаточную функцию реального дифференцирующего звена для удобства получения временных характеристик –

.

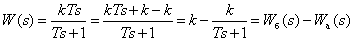Временные характеристики можно определить по известным характеристикам безынерционного и апериодического звеньев –

,

.

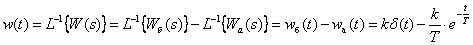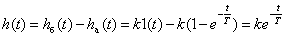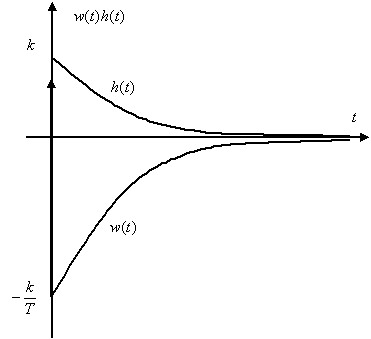
Частотная характеристика

,

.

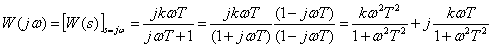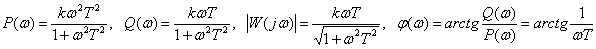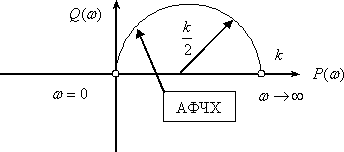
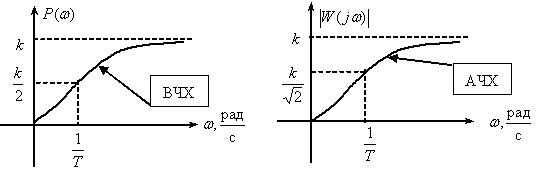
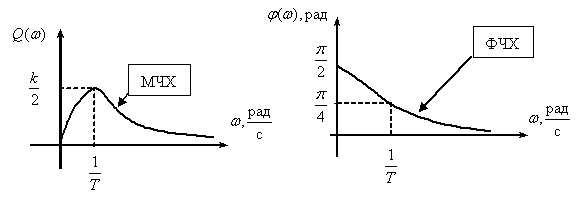
Интегрирующее звено с запаздыванием

Передаточная функция

.

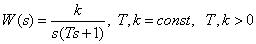Преобразуем передаточную функцию реального дифференцирующего звена для удобства получения временных характеристик –

,

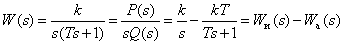где

.

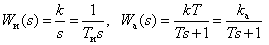Временные характеристики можно определить по известным характеристикам интегрирующего и апериодического звеньев –

,

.

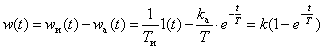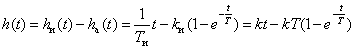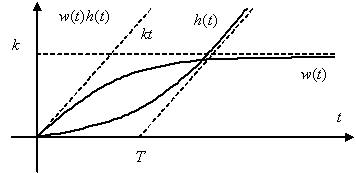
Частотная характеристика

,

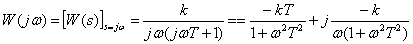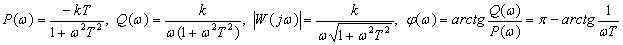
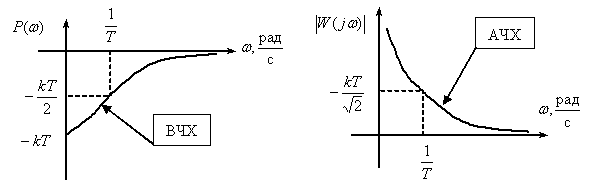
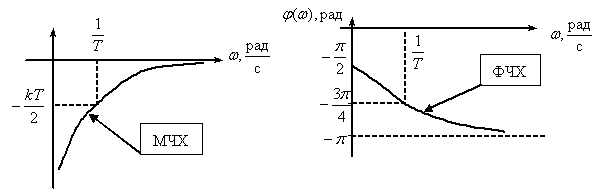
Пропорционально-интегрирующее звено

Передаточная функция

.

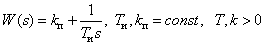Временные характеристики можно определить по известным характеристикам безынерционного и интегрирующего звеньев –

,

.

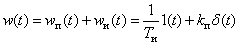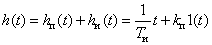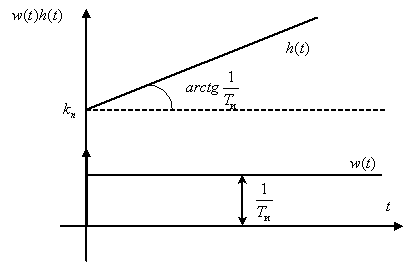
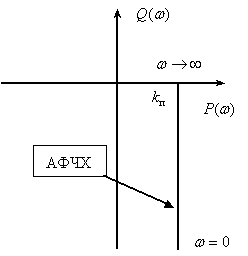
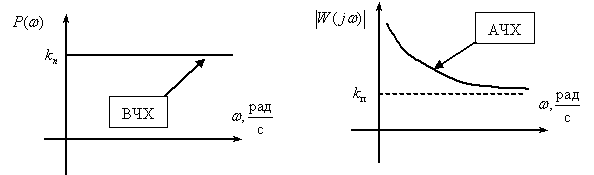
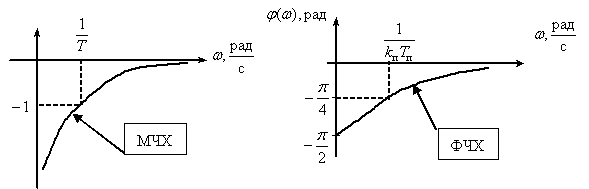
Частотная характеристика

,

.

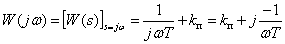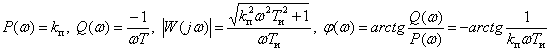Контрольные вопросы и задачи

1. Сравните характеристики дифференцирующего и реально дифференцирующего звеньев. Что в них общего, и чем они отличаются?

2. Сравните характеристики интегрирующего звена и интегрирующего звена с запаздыванием. Что в них общего, и чем они отличаются?

3. Дифференциальное уравнение, описывающее динамическое звено имеет вид –

.

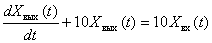Определите передаточную функцию типового динамического звена и его название.

Ответ:

Имеем апериодическое звено с передаточной функцией –

,

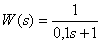4. Передаточная функция динамического звена имеет вид –

,

как измениться амплитуда гармонического сигнала с частотой 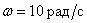во сколько раз?

Ответ:

Сигнал уменьшится в 10 раз.

5. Передаточная функция динамического звена имеет вид –

,

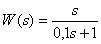как измениться фаза гармонического сигнала с частотой ?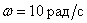

Ответ:

Выходной сигнал будет опережать входной на .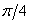

6. Передаточная функция динамического звена имеет вид –

,

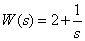Определите угол наклона переходной характеристики этого звена.

Ответ:

Угол наклона составляет 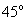.