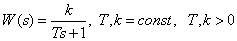Лекция 10

Логарифмические частотные характеристики систем автоматического управления

Апериодическое звено

Передаточная функция –

.

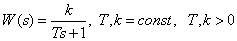Частотная характеристика –

,

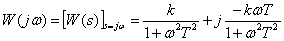АЧХ и ФЧХ

.

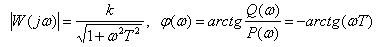Логарифмические характеристики

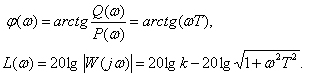
В этом случае, при частоте –

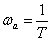
имеем

.

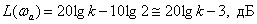Рассмотри для апериодического звена два характерных диапазона:

,

.

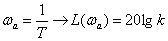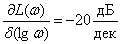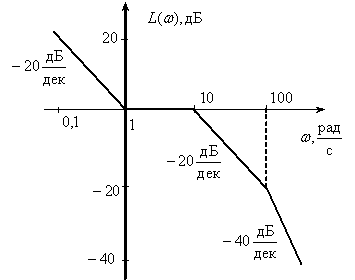
Выражения (1) и (2) представляют собой уравнения прямых линий – асимптот, к которым стремиться ЛАЧХ при удалении от точки их сопряжения 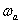. Как мы увидим в дальнейшем, при синтезе и анализе систем бывает удобнее пользоваться не точными, а асимптотическими характеристиками.

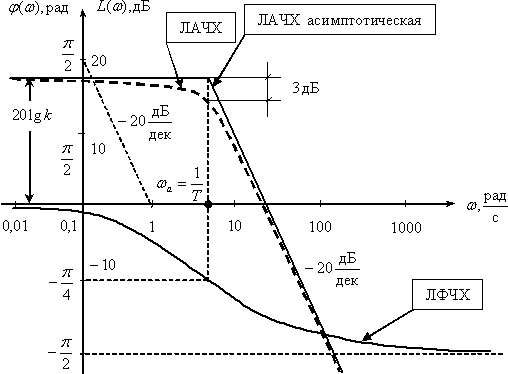
Как мы увидели при работе с простейшими типовыми звеньями, частотные характеристики могут быть получены по передаточной функции. В более сложных случаях, при решении задач синтеза и анализа САУ возникает потребность в получении характеристик САУ по известным характеристикам звеньев, входящих в САУ.

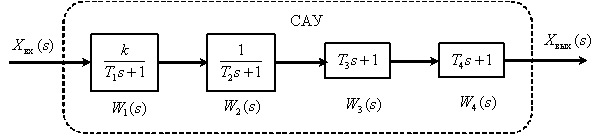
Наиболее часто используется случай, когда звенья в САУ включаются последовательно, как это показано на рис. 1.

Рис. 1

В соответствии с правилами эквивалентных преобразований передаточная функция всей САУ будет иметь вид –

.

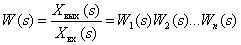Получим частотную характеристику САУ

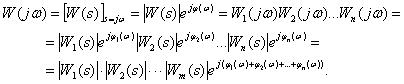
Следовательно,

АЧХ САУ –

ФЧХ САУ

Получим по выражениям (3) и (4) логарифмические характеристики САУ:

ЛАЧХ –

ЛФЧХ –

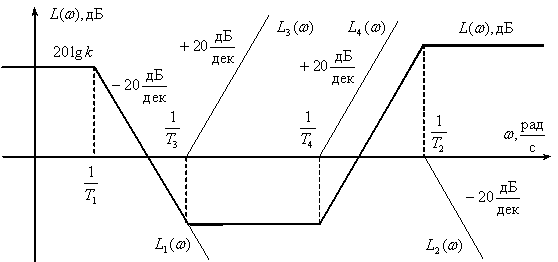
Таким образом, логарифмические частотные характеристики САУ могут быть определены, как сумма логарифмических частотных характеристик последовательно включенных составляющих САУ звеньев. Логарифмические масштабы и использование асимптот позволяет осуществить суммирование графически.

В ТАУ так же используются свойства логарифмических частотных характеристик динамических звеньев, передаточные функции которых взаимообратные –

.

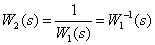Пусть частотные характеристики звена 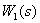известны:

Частотная характеристика –

,

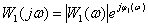ЛАЧХ –

,

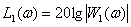ЛФЧХ –

.

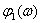Тогда частотные характеристики звена 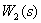имеют вид:

Частотная характеристика –

,

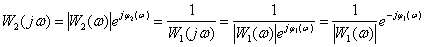ЛАЧХ –

,

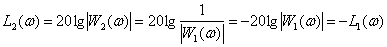ЛФЧХ –

.

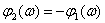Таким образом, ЛАЧХ и ЛФЧХ взаимообратных динамических звеньев расположены симметрично относительно оси частот, подтверждением чему служат полученные ранее ЛАЧХ и ЛФЧХ дифференцирующего и интегрирующего звеньев.

Пример

Для САУ была определена передаточная функция. Следует определить ЛАЧХ САУ.

.

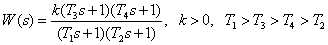Решение

Представим САУ в виде последовательно включенных динамических звеньев

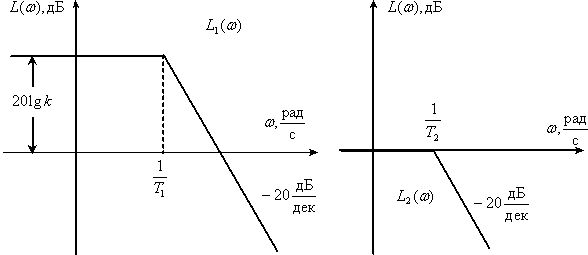
Получим асимптотические ЛАЧХ для каждого апериодического звена

Используя свойства ЛАЧХ взаимообратных звеньев, получим асимптотические ЛПЧХ форсирующих звеньев .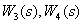

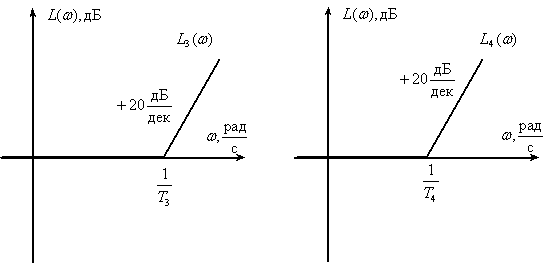
Получим асимптотическую ЛАЧХ САУ выполнив графическое суммирование ЛАЧХ звеньев

.

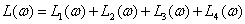Задачу существенно упрощает то, что асимптотические графики звеньев имеют участки с целочисленным наклоном.

Получим ЛАЧХ и ЛФЧХ типовых звеньев, используя рассмотренное выше.

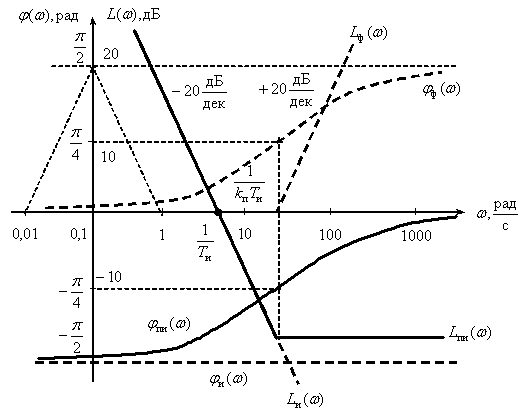
Реальное дифференцирующее звено

Передаточная функция

.

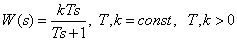Представим звено в следующем виде

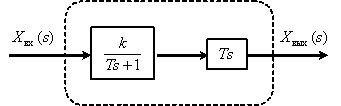
Тогда ЛАЧХ и ЛФЧХ имеют вид –

,

.

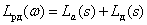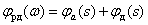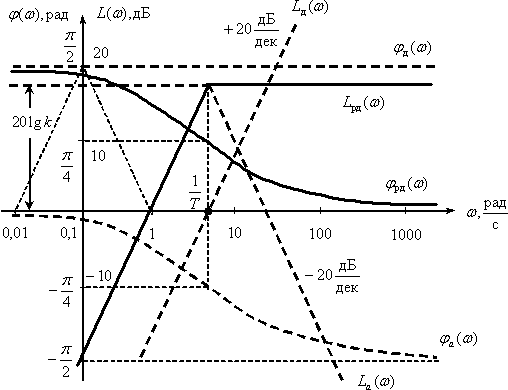
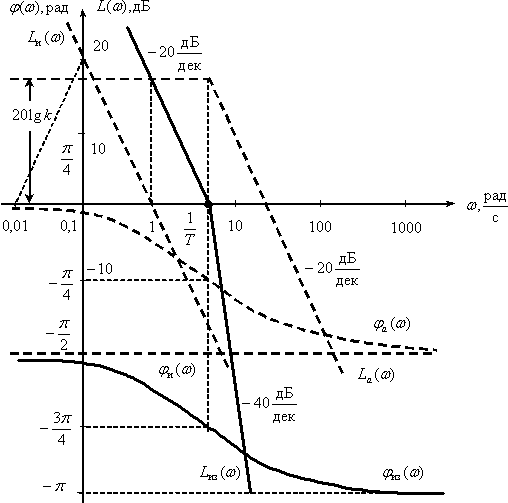
Интегрирующее звено с запаздыванием

Передаточная функция

.

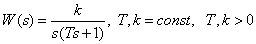Представим звено в следующем виде

Тогда ЛАЧХ и ЛФЧХ имеют вид –

,

.

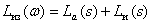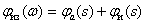Пропорционально-интегральное звено

Передаточная функция

.

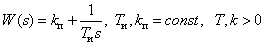Представим звено в следующем виде

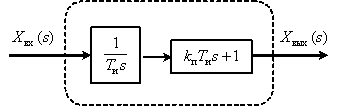
Тогда ЛАЧХ и ЛФЧХ имеют вид –

,

.

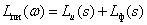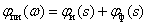Контрольные вопросы и задачи

1. Как можно использовать для получения частотных характеристик системы то, что систему можно представить в виде параллельно включенных типовых динамических звеньев?

2. Как соотносятся ЛАЧХ и ЛФЧХ динамических звеньев, передаточные функции которых являются взаимообратными?

3. На какие последовательно включенные типовые динамические звенья следует разбить реально дифференцирующее звено, чтобы получить его асимптотическую ЛАЧХ и ЛФЧХ?

4. На какие последовательно включенные типовые динамические звенья следует разбить интегрирующее звено с запаздыванием, чтобы получить его асимптотическую ЛАЧХ и ЛФЧХ?

5. На какие последовательно включенные типовые динамические звенья следует разбить пропорционально интегрирующее звено, чтобы получить его асимптотическую ЛАЧХ и ЛФЧХ?

6. Передаточная функция звена –

,

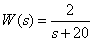При какой частоте ЛФЧХ будет иметь значение .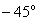

Ответ:

При частоте.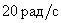

7. Передаточная функция звена –

,

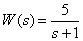Как при частоте 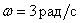будут отличаться точная и асимптолическая ЛАЧХ этого звена?

Ответ:

Асимптотическая ЛАЧХ будет меньше точной на .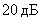

8. Передаточная функция объекта имеет вид –

,

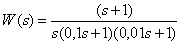Постройте асимптотическую ЛАЧХ объекта?

Ответ: