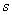 имеет следующий вид:
имеет следующий вид:Лекция 1
Введение
Цель преподавания дисциплины состоит в том, чтобы дать студентам достаточно полное представление об основных концепциях и принципах получения, преобразования и анализа различных видов математических моделей, используемых в теории автоматического управления для описания объектов управления различной природы и систем управления различных классов. Кроме того, студенты должны овладеть навыками решения практических задач, связанных с математическим моделированием в теории автоматического управления, рационально используя математический аппарат.
Широкий набор методов анализа и синтеза систем автоматического управления, различных форм представления математических моделей объектов различной природы, используемых специалистами и бакалаврами, требует решения в рамках дисциплины Математические основы теории автоматического управления (МОТАУ) следующих задач:
углубление знаний и формализация представлений в области основ математического описания систем автоматического управления, таких разделов высшей математики как дробно-рациональные функции комплексного переменного, импульсные функции, преобразования Фурье и Лапласа, операторный метод решения дифференциальных уравнений, линейная алгебра;
формирование знаний и практических навыков получения и преобразования различных форм математических моделей динамических звеньев и систем автоматического управления в целях их рационального использования при решении задач анализа и синтеза систем управления;
изучение специфики методов получения и преобразования математических моделей многомерных объектов управления, базирующихся на аппарате линейной алгебры и представлении объектов в пространстве состояний;
изучение методов оценки качества процессов в системах автоматического управления, формирование практических навыков по использованию различных критериев качества переходных процессов при анализе и синтезе систем автоматического управления;
формирование понятий и практических навыков решения задач идентификации элементов САУ.
Изучение дисциплины базируется на том, что студент имеет соответствующую математическую подготовку в области дифференциального и интегрального исчислений, линейной алгебры, комплексных чисел и тригонометрических функций, а также знаком с основными понятиями и законами, рассматриваемыми в курсах теоретических основ электротехники и теоретической механики. Обучение в 4 семестре происходит параллельно с изучением ТОЭ (часть 2), в 5 семестре – с изучением ТАУ (часть 1).
Дисциплина рассчитана на изучение в течение 4 и 5 семестров (2 и 3 курс), включает в свой состав 42 лекционных часа, 28 часов практических занятий и 14 часов лабораторного практикума (в 5 семестре).
Дисциплина включает в себя следующие основные разделы:
основы математического описания систем автоматического управления,
виды математических моделей динамических звеньев,
математические модели элементарных динамических звеньев,
математические модели САУ,
особенности математических моделей многомерных систем автоматического управления,
методы оценки качества систем автоматического управления,
идентификация параметров математической модели систем автоматического управления.
Дробно-рациональные функции
Дробно-рациональные функции комплексного переменного в различных формах широко используют в ТАУ для представления передаточных функций и решения задач синтеза и анализа САУ.
Дробно-рациональная функция некоторого действительного или комплексного переменного 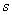 имеет следующий вид:
имеет следующий вид:
|
|
(1) |
где 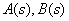 - полиномы числителя и знаменателя,
- полиномы числителя и знаменателя, 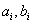 - действительные числа,
- действительные числа, 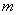 - порядок числителя,
- порядок числителя, 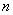 - порядок знаменателя (всей дробно-рациональной функции функции),
- порядок знаменателя (всей дробно-рациональной функции функции), 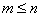 - для функций используемых в ТАУ.
- для функций используемых в ТАУ.
Полиномы дробно-рациональной функции могут быть представлены в виде произведения биномов (разложение многочлена на сомножители), тогда функция может быть представлена в форме Боде
|
|
(2) |
где 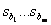 - корни уравнения
- корни уравнения 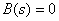 ,
, 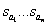 - корни характеристического уравнения
- корни характеристического уравнения 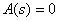 .
.
Корни уравнения 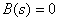 называют нулями дробно-рациональной функции
называют нулями дробно-рациональной функции 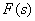 , так как
, так как
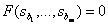 .
.
Корни характеристического уравнения 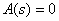 называют полюсами дробно-рациональной функции, так как
называют полюсами дробно-рациональной функции, так как
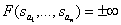 .
.
Полюсы и нули могут быть действительными и комплексно-сопряженными числами. Таким образом, задача представления функции в форме Боде сводится к поиску корней уравнений, образованных полиномами числителя и знаменателя.
Их принято располагать на плоскости комплексной переменной 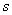 , обозначая расположение полюсов крестиками, а нулей кружками. Для лучшего освоения этого материала необходимо освежить в памяти сведения из высшей математики по операциям с комплексными числами. Нули, а особенно полюсы дробно-рациональных функций изображают на плоскости комплексного переменного
, обозначая расположение полюсов крестиками, а нулей кружками. Для лучшего освоения этого материала необходимо освежить в памяти сведения из высшей математики по операциям с комплексными числами. Нули, а особенно полюсы дробно-рациональных функций изображают на плоскости комплексного переменного 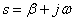 . На рис. 1 показано расположение полюсов и нулей некоторой дробно-рациональной функции.
. На рис. 1 показано расположение полюсов и нулей некоторой дробно-рациональной функции.
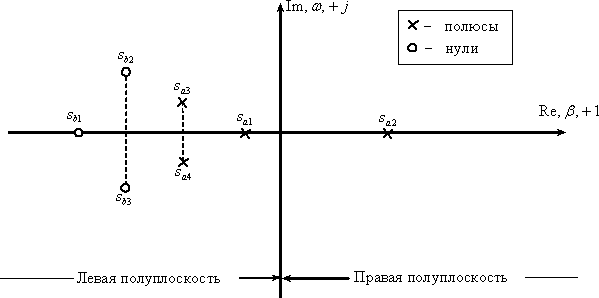
Рис. 1
Мнимая ось делит плоскость 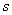 на правую и левую полуплоскости. Нули и полюсы, расположенные в правой полуплоскости, называют правыми, в левой полуплоскости – левыми. Комплексные полюсы и нули всегда располагаются парами симметрично относительно действительной оси; такие пары корней называют комплексно сопряженными корнями. Если среди нулей и полюсов встречаются два или несколько одинаковых, их называют кратными в отличие от остальных, которых называют простыми. Кратность определяется числом одинаковых нулей или полюсов (
на правую и левую полуплоскости. Нули и полюсы, расположенные в правой полуплоскости, называют правыми, в левой полуплоскости – левыми. Комплексные полюсы и нули всегда располагаются парами симметрично относительно действительной оси; такие пары корней называют комплексно сопряженными корнями. Если среди нулей и полюсов встречаются два или несколько одинаковых, их называют кратными в отличие от остальных, которых называют простыми. Кратность определяется числом одинаковых нулей или полюсов (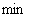 – 2). Рассмотрим пример получения формы Боде.
– 2). Рассмотрим пример получения формы Боде.
Пример
Представьте дробно-рациональную функцию
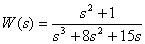
в форме Боде и покажите расположение полюсов и нулей дробно-рациональной функции на комплексной плоскости.
Решение
Найдем корни уравнения
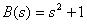 .
.
Получаем два комплексно-сопряженных корня (нуля)
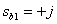 ,
, 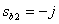 .
.
Найдем полюсы 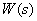
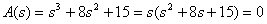 .
.
Получаем три полюса
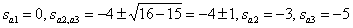 .
.
Покажем расположение нулей и полюсов на комплексной плоскости (см. рис. 2).
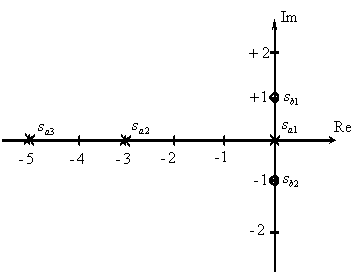
Рис. 2
Дробно-рациональную функцию (1) часто представляют в виде суммы простейших дробей (форма Хэвисайта)
|
|
(3) |
где  - корни характеристического уравнения
- корни характеристического уравнения 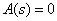 ,
, 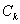 - коэффициенты разложения, которые находят по следующей функции:
- коэффициенты разложения, которые находят по следующей функции:
|
|
(4) |
Такое представление дробно-рациональной функции возможно, если полюсы 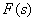 – простые, а
– простые, а 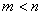 .
.
Функция, которая имеет один нулевой полюс, может быть представлена в следующем виде:
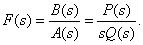
В этом случае вместо формул (3), (4) применяют выражение
|
|
(5) |
где  - ненулевые полюсы
- ненулевые полюсы 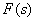 , корни уравнения
, корни уравнения 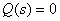 ,
,
|
|
(6) |
Следовательно, представление дробно-рациональной функции в форме Хэвисайта сводится к нахождению полюсов дробно-рациональной функции и рациональному использованию формул разложения. Рассмотрим ряд примеров получения формы Боде.
Пример
Представьте дробно-рациональную функцию
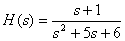
в форме Хэвисайта, используя формулы разложения (3), (4).
Решение
Уравнение полинома числителя имеет вид
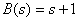 .
.
Характеристическое уравнение имеет вид
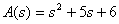 .
.
Найдем корни характеристического уравнения
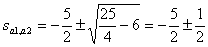 ,
, 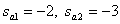 .
.
Определим производную от полинома знаменателя
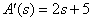 .
.
Определим коэффициенты разложения соответствующие по номеру полюсам
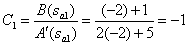 ,
, 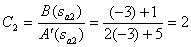 .
.
Тогда форма Хэвисайта имеет вид
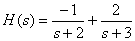 .
.
Пример
Представьте дробно-рациональную функцию
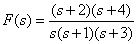
в форме Хэвисайта, используя формулы разложения (5), (6).
Решение
Представим 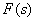 в виде
в виде
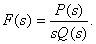
Тогда
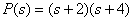 ,
,
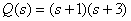 .
.
Ненулевые полюсы имеют вид
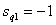 ,
, 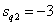 .
.
Производная от 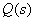
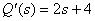 .
.
Определим коэффициенты разложения
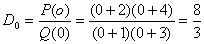 ,
,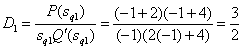 ,
,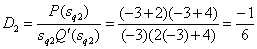 .
.
Тогда форма Хэвисайта имеет вид
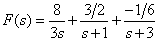 .
.
Импульсные функции
Реальные сигналы (переменные и воздействия), встречающиеся в системах управления, обычно представляют с помощью некоторых идеализаций – импульсных функций. Чаще всего используют ступенчатую единичную функцию (функцию Хэвисайта) и дельта-функцию (функцию Дирака), которые описываются следующим образом:
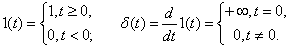
Графики этих функций показаны на рис. 3.
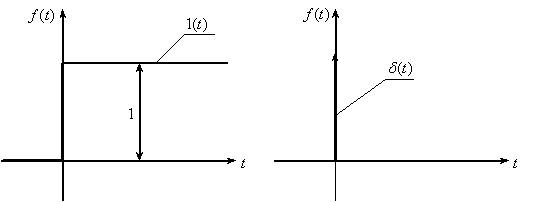
Рис. 3
Для единичной и дельта-функции справедливо
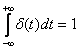 .
.
Таким образом, дельта-функция представляет собой мгновенный импульс, равный бесконечности в нулевой момент времени и нулю в другие моменты, площадь которого постоянна и равна единице. Поэтому иногда 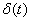 называют единичным импульсом.
называют единичным импульсом.
Контрольные вопросы и задачи
Как определить порядок дробно-рациональной функции?
Поясните процедуру преобразования функции к форме Боде.
Какие полюсы дробно-рациональной функции называют простыми?
В чем состоит идеализация представления реального сигнала единичной ступенчатой функцией?
Представьте дробно-рациональную функцию
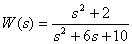
в форме Боде.
Ответ:
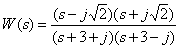 .
.
Представьте дробно-рациональную функцию
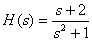
в форме Хэвисайта.
Ответ:
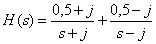 .
.
Представьте дробно-рациональную функцию
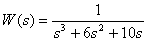
в форме Хэвисайта.
Ответ:
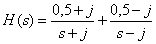 .
.