Лекция No 9.

Тема: «Структурные модели автономных инверторов напряжения (АИН)»

9.1. Логическая модель автономного инвертора

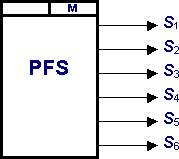
Имитация различных алгоритмов управления автономным инвертором возможна с помощью специального блока переключающих функций PFS, внешнее представление которого представлено на рис. 9.1. Функциональный блок PFS имеет 6 выходных сигналов S₁, S₂, S₃, S₄, S₅, S₆, которые идентифицируют состояния ключей V₁, V₂, V₃, V₄, V₅, V₆, принимая значения S_i=1 при замкнутом состоянии i–го ключа и S_i=0 - при разомкнутом состоянии i–го ключа. Частота переключения является внутренним параметром блока.

Рис. 9.1. Внешнее представление функционального блока PFS

Изменение алгоритма управления инвертором требует изменения внутренней структуры функционального блока PFS. Так, для наиболее применимого алгоритма управления ключами инвертора «по шестиугольнику», когда осуществляется циклический переход

, …,

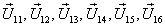диаграмма выходных сигналов блока S₁, S₂, S₃, S₄, S₅, S₆ приведена на рис. 9.2.

Рис. 9.2. Диаграмма выходных сигналов блока PFS

На основании информации, содержащейся в таблице состояний инвертора (см. предыдущую лекцию) составляющие вектора 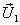в системе координат 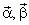могут быть определены с помощью следующих логических уравнений:

Логические уравнения (9.1) положены в основу внутреннего представления функционального блока вычисления напряжений 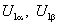- ALBETA, схема которого приведена на рис. 9.3.

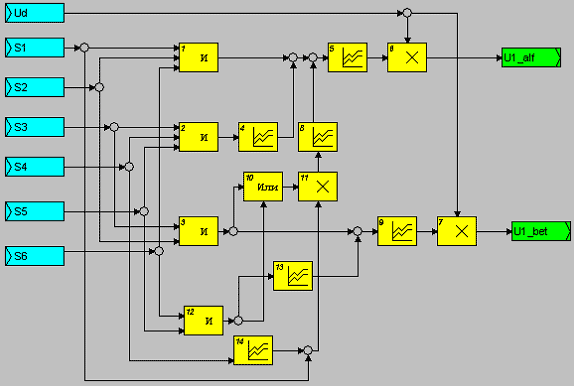
Рис. 9.3. Схема внутреннего представления функционального блока ALBETA

9.2. Вычисление тока в цепи постоянного напряжения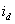

Определенный класс исследовательских и проектных задач систем с автономными инверторами требуют изучения характера изменения тока в цепи постоянного напряжения. Как видно из силовой схемы инвертора (см. рис. 8.1 в предыдущей лекции), мгновенные значения тока 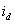определяются значениями токов

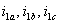
фаз нагрузки и состоянием ключей автономного инвертора. Результаты определения значений токов для каждого из восьми возможных состояний инвертора приведены в таблице состояний инвертора (см. предыдущую лекцию).

Сопоставляя выражения для токов 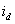с состояниями ключей АИН, характеризующимися булевыми переменными S₁, S₂, S₃, S₄, S₅, S₆ можно получить обобщенное логическое уравнение вычисления тока:

или

где

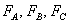
– логические функции, представленные в уравнении (9.2).

Для определения логических функций построен функциональный блок FF, схема внутреннего представления которого приведена на рис. 9.4.

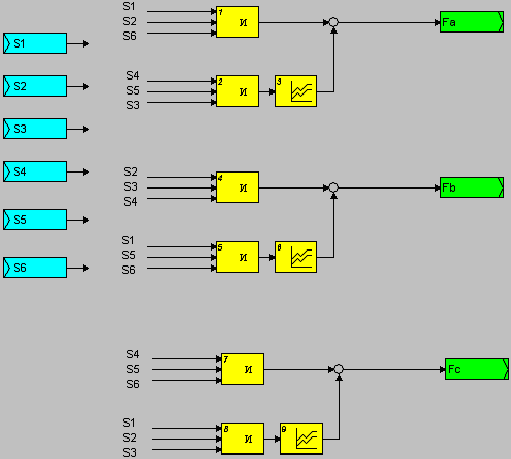
Рис. 9.4. Внутренняя схема функционального блока ALBETA

Вычисление тока 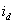производится с помощью функционального блока MID, схема внутреннего представления которого приведена на рис. 9.5.

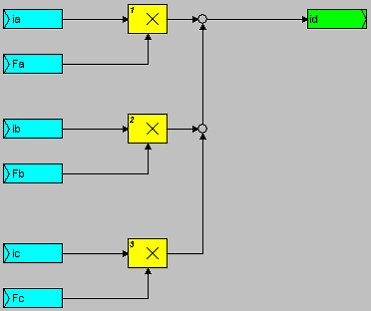
Рис. 9.5. Схема внутреннего представления функционального блока MID

9.3. Матричная модель АИН

Формально процесс получения составляющих выходного напряжения автономного инвертора в различных системах координат в зависимости от алгоритма управления и величины напряжения звена постоянного тока может быть описан с помощью матриц преобразования, как это показано на рис. 9.6., где приведена общая структура матричной модели инвертора.

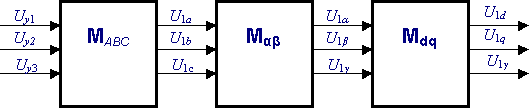
Рис. 9.6. Матричная модель АИН

Входным сигналом модели является единичный вектор управления

задающий пространственное расположение векторов выходного напряжения инвертора в системе координат A, B, C.

Переход от вектора управления к реальным фазным напряжениям осуществляется с помощью матрицы M_ABC

Таким образом, алгоритм переключения ключей АИН здесь неявно задается коэффициентами матрицы M_ABC. Так для алгоритма управления «по шестиугольнику», временные диаграммы связи составляющих векторов 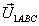и 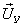приведены на рис. 9.7, матрица M_ABCимеет следующий вид:

a)

15%

b)

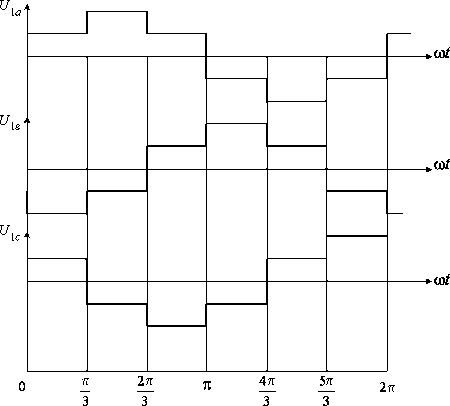
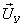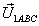Рис. 9.7. Временные диаграммы составляющих векторов (а) и (б)

Для использования в качестве нагрузки АИН модели асинхронного электродвигателя, построенной в системе координат 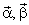, необходимо перейти к новой неподвижной системе координат с базисом 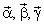. Матрица перехода к ней имеет вид:

Тогда напряжение статора в системе координат 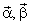получается как

С помощью матрицы перехода

можно получить значения составляющих напряжения статора в системе координат d,q

Здесь 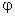– угол поворота ротора в системе координат.

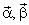Контрольные вопросы к лекции No 9.

1. Какие типы логических элементов должны быть использованы в логической модели АИН? Определите число элементов каждого типа.

2. Сколько и какие значения принимает составляющая вектора 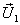по оси - .

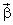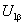3. Укажите основные особенности формирования матричной модели АИН для подключения к модели АД в системе координат d, q.

ОТВЕТЫ