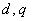Лекция No 7.

Тема: Построение структурной модели электромеханического преобразования энергии в асинхронном электродвигателе для системы координат d,q »

Для неподвижной относительно ротора системы координат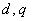, вращающейся в пространстве со скоростью

,

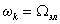дифференциальные уравнения электрического равновесия напряжений в обмотках принимают следующий вид

Четыре уравнения системы (7.1) содержат восемь линейно зависимых переменных. В этой связи, здесь, прежде всего необходимо, с помощью выражений связи токов и потоко сцеплений обмоток статора и ротора (см. (5.2) в лекции No 5)

исключить две пары переменных, то есть выбрать состав компонент вектора .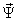

Следует отметить, что выбрать состав компонент вектора нужно так, чтобы результирующее математическое описание электромеханического преобразования энергии в АД не содержало бы алгебраических уравнений, а, следовательно, структурная модель не имела бы безынерционных контуров. Выберем следующий состав компонент вектора :

.

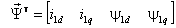Из первых двух уравнений системы (7.2) выразим токи ротора

Полученные выражения (7.3) подставим в уравнения для потокосцеплений ротора, то есть в два последних уравнения системы (7.2)

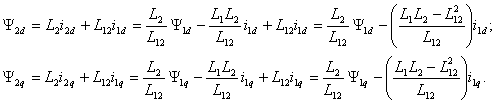
Обозначив

,

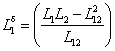получим выражения для потокосцеплений обмоток ротора:

Далее выражения (7.3) подставим в уравнения системы (7.1) и с учетом обозначения

,

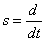получим

Примем

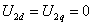
и преобразуем (7.5) к виду, удобному для построения структурной модели

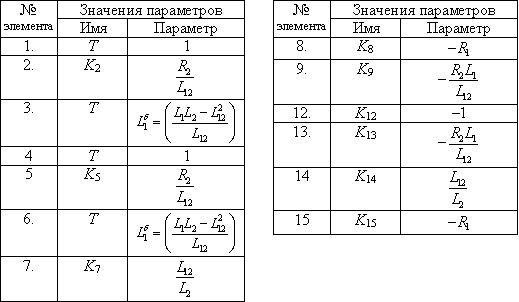
С помощью полученных уравнений можно легко построить внутренне представление функционального блока ЕМР_DQ. Схема этого представления приведена на рис. 7.1, а расшифровка параметров динамических элементов представлено в таблице 7.1.

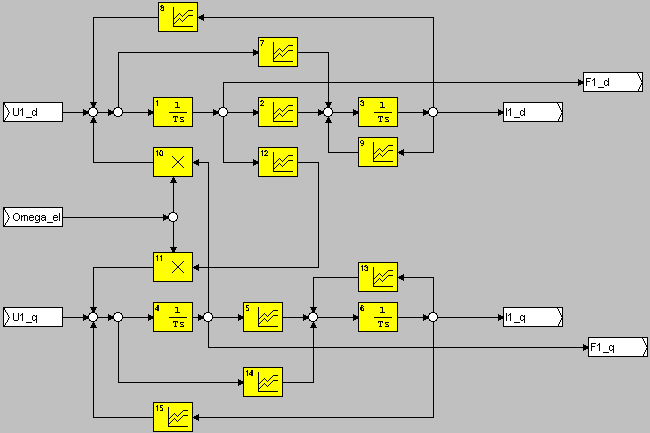
Рис. 7.1. Внутренняя схема функционального блока ЕМР_DQ

Таблица 7.1. Параметры элементов функционального блока ЕМР_DQ

Для выбранного состава компонент вектора 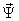внутренняя структура блока формирования электромагнитного момента принимает вид, приведенный на рис. 7.2.

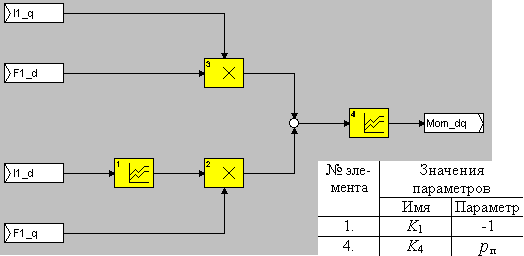
Рис. 7.2. Внутренняя схема функционального блока Moment_dq

Для формирования составляющих напряжения статора в системе координат d,q воспользуемся формулами преобразования, которые в общем виде получены в лекции 3 (3.3)

Выражения (7.7) положены в основу внутреннего представления дополнительного функционального блока DQ (рис.7.3).

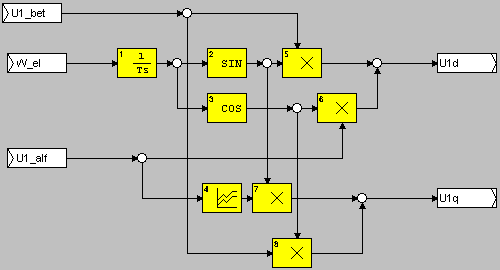
Рис. 7.3. Схема внутреннего представления функционального блока DQ

С учетом вышеизложенного, структурная модель функционального уровня асинхронного электродвигателя, построенная в систем координат d,q, принимает вид, приведенный на рис. 7.4.

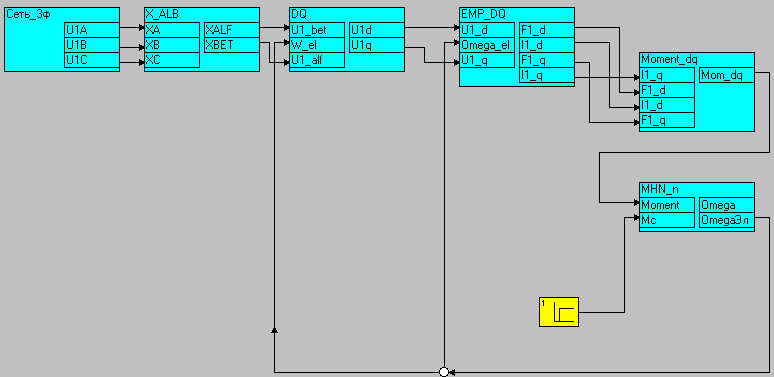
Рис. 7.4. Структурная модель АД в системе координат d,q

Контрольные вопросы к лекции No 7

1. Из каких соображений следует выбирать состав компонент вектора 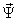при построении модели АД системе координат d,q?

2. Каким образом в функциональном блоке решается проблема вычисления мгновенных значений производных пототокосцеплений статора

?

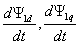3. Укажите основное отличие структурной модели функционального уровня АД в системе координат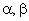 от такой же модели в системе координат d,q?

ОТВЕТЫ