Лекция No 6.

Тема: Построение структурной модели электромеханического преобразования энергии в асинхронном электродвигателе для системы координат »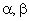

Наибольший практический интерес представляют структурные модели асинхронного электродвигателя, построенные в неподвижной ортогональной системе координат 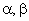. Это объясняется, прежде всего, тем, что указанные модели могут быть использованы для имитационного моделирования систем, в которых АД подключается к источникам несинусоидального напряжения (автономным инверторам, статическим преобразователям частоты и т.п.).

Для неподвижной относительно статора системы координат

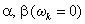
дифференциальные уравнения электрического равновесия напряжений в обмотках статора и ротора машины принимают следующий вид

Четыре уравнения системы (6.1) содержат восемь линейно зависимых переменных. В этой связи, здесь, прежде всего необходимо, с помощью выражений связи токов и потоко сцеплений обмоток статора и ротора (см. (5.2) в предыдущей лекции)

исключить две пары переменных, то есть выбрать состав компонент вектора .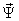

Следует отметить, что выбрать состав компонент вектора 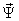нужно так, чтобы результирующее математическое описание электромеханического преобразования энергии в АД не содержало бы алгебраических уравнений, а, следовательно, структурная модель не имела бы безынерционных контуров. Выберем следующий состав компонент вектора :

.

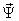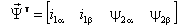Из двух последних уравнений системы (6.2) выразим токи ротора

Полученные выражения (6.3) подставим в уравнения для потокосцеплений статора, то есть в первые два уравнения системы (6.2)

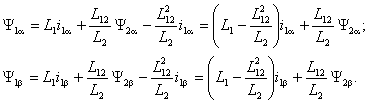
Обозначив

,

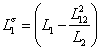получим выражения для потокосцеплений обмоток статора:

Далее выражения (6.3) подставим в уравнения системы (6.1) и с учетом обозначения

,

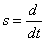получим

Преобразуем (6.5) к виду, удобному для построения структурной модели

С помощью полученных уравнений можно легко построить внутренне представление функционального блока ЕМР. Схема этого представления приведена на рис. 6.1, а расшифровка параметров динамических элементов представлено в таблице 6.1.

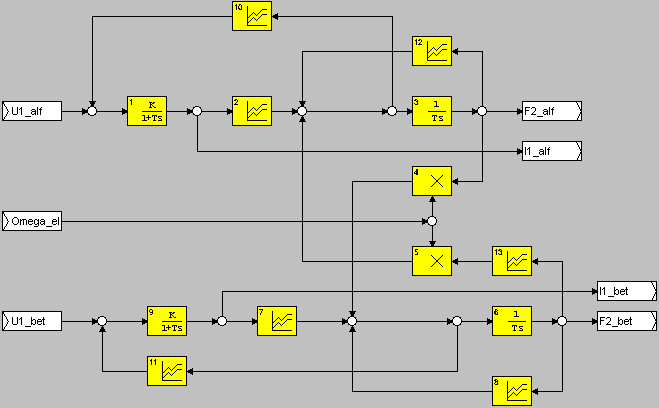
Рис. 6.1. Внутренняя схема функционального блока ЕМР

Таблица 6.1. Параметры элементов функционального блока ЕМР

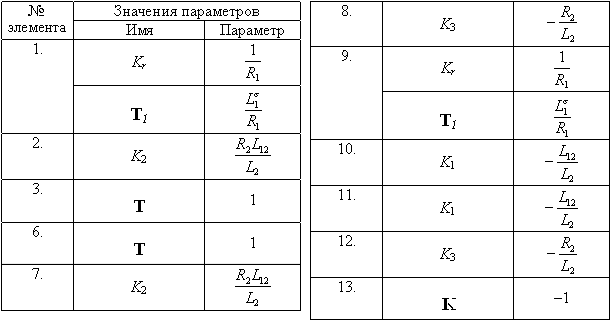
Для выбранного состава компонент вектора 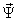внутренняя структура блока формирования электромагнитного момента принимает вид, приведенный на рис. 6.2.

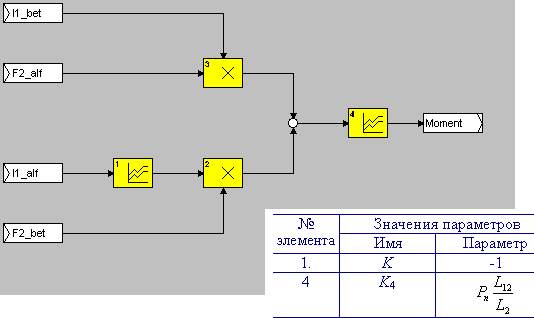
Рис. 6.2. Внутренняя схема функционального блока М

С учетом вышеизложенного, структурная модель функционального уровня асинхронного электродвигателя, построенная в систем координат 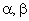, принимает вид, приведенный на рис. 6.3.

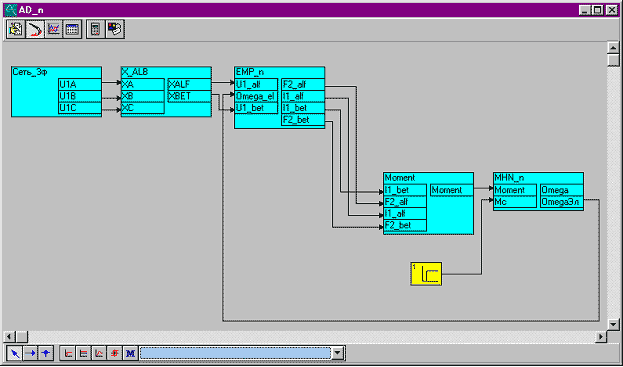
Рис. 6.3. Структурная модель АД в системе координат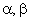

Результаты имитационного эксперимента прямого пуска имитационного эксперимента с использованием построенной структурной модели приведены на рис. 6.4. Конкретные значения и методику расчета параметров электродвигателя, его модели и можно найти в методических указаниях к лабораторному практикуму [3]

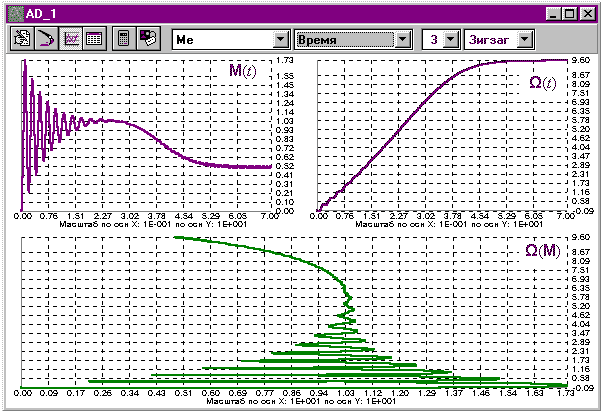
Рис. 6.4. Результаты испытания модели АД в системе координат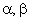

Контрольные вопросы к лекции No 6.

1. Из каких соображений следует выбирать состав компонент вектора 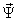при построении модели АД системе координат ?

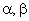2. Какие динамические элементы указывают на нелинейных характер модели АД в системе координат 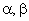? В каких функциональных блоках они присутствуют?

3. При каких значениях и характере (активный или реактивный) момента статического сопротивления выполнен имитационный эксперимент, результаты которого приведены на рис. 6.4?

ОТВЕТЫ