Лекция No 4.

Тема: «Фазные преобразования переменных. Выбор скорости вращения координатных осей u,v »

Математическое описание динамических процессов получено для двухфазной электрической машины. Реальные электродвигатели переменного тока чаще всего имеют трехфазную обмотку статора, поэтому возникает необходимость преобразования переменных трехфазной машины к переменным двухфазной модели и наоборот. Основой для такого преобразования может служить физический смысл координатных преобразований. Действительно, один и тот же результирующий вектор МДС может быть создан как двухфазной, так и трехфазной обмоткой, поэтому для получения формул двухфазно-трехфазных преобразований будем использовать тот же принцип, что и для получения формул координатных преобразований, рассмотренный в предыдущей лекции.

Решим задачу преобразования реальных переменных

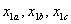
статора трехфазной машины к ортогональной системе координат 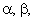то есть к реальным переменным статора эквивалентной двухфазной машины.

Разница в числе фаз затрудняет выполнение условия инвариантности мощности. Учитывая это, представим реальные переменные трехфазной машины в виде векторов, и будем полагать, что преобразованные переменные в осях 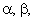не равны, а пропорциональны сумме проекций реальных переменных

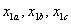
на оси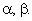

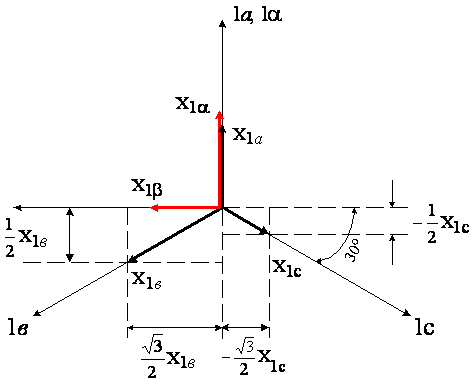
Рис. 4.1. Схема преобразования переменных трех фазного электродвигателя

На основании построений, приведенных на рис. 4.1, можно записать

где k_c – согласующий коэффициент пропорциональности, выбор которого осуществляется из условия инвариантности мощности.

Рассмотрим наиболее распространенный на практике случай, когда переменные трехфазной машины подчиняются условию:

С учетом (3.2) можно записать

Переменные

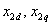
для роторной цепи машины также определяются выражениями (4.3) и (4.4) при соответствующей замене индексов.

Формулы обратного образования можно получить аналогично

Для определения согласующего коэффициента k_c используем равенство суммарной мгновенной мощности, потребляемой обмотками статора реальной и обобщенной машинами.

Выразим с помощью (4.4) составляющие мгновенной мощности трехфазной машины

Следовательно, для выполнения условия инвариантности мощности согласующий коэффициент должен иметь значение

при этом

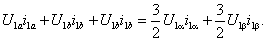
Подставляя (4.6) в (4.3),

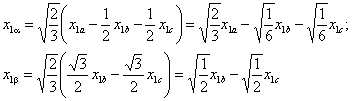
получим формулы прямого преобразования

Матричная форма указанных формул принимает следующий вид:

Запишем так же и формулы обратного преобразования.

или в матричной форме

Рассмотренные преобразования переменных обобщенной электрической машины в значительной степени облегчают анализ динамических режимов электропривода и во многих случаях позволяют при моделировании на ЭВМ вместо реальных переменных токов и напряжений оперировать соответствующими им после преобразования постоянными величинами. Это удается достичь удачным выбором скорости вращения координатных осей u,v.

Выбор

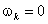
обеспечивает преобразование реальных переменных ротора, выраженных в осях 2d, 2q, к неподвижным осям

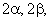
связанным со статором машины. Уравнения электрического равновесия напряжений в обмотках статора и ротора в этом случае имеют вид:

При этом преобразовании напряжения и токи обмоток остаются переменными, но имеют одинаковую частоту, равную частоте сети.

Вариант

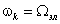
соответствует преобразование реальных переменных машины к осям d, q, жестко связанным с ротором машины. Уравнения электрического равновесия напряжений в обмотках статора и ротора в этом случае имеют вид:

Здесь также напряжения и токи обмоток являются переменными, но имеют как в статоре, так и в роторе частоту

,

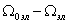т.е. частоту тока ротора.

Если принять

,

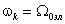можно выразить все переменные системы в осях x,y, вращающихся с синхронной скоростью машины. Уравнения электрического равновесия напряжений в обмотках статора и ротора в этом случае имеют вид:

При этом к реальным обмоткам статора приложена симметричная двухфазная система напряжений

С помощью формул прямого преобразования, приведенных в предыдущей лекции (3.3), положив

,

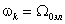преобразуем напряжения

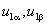
в соответствующие им напряжения u_1x, u_1y:

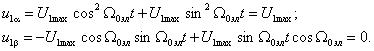
Таким образом, в системе координат x,y реальные переменные напряжения, приложенные к обмоткам статора, преобразуются в постоянное напряжение U_1max=const, приложенное к оси x. Этот результат имеет очевидный физический смысл: вращающееся магнитное поле, создаваемое при неподвижных обмотках статора, переменными напряжениями

,

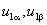при переходе к обмоткам, вращающимся со скоростью поля, может быть создано только постоянным напряжением.

Контрольные вопросы к лекции No 4.

1. Почему считается, что преобразованные переменные в осях 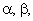не равны, а пропорциональны сумме проекций реальных переменных 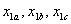на оси ?

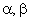2. Какие условия используются для определения значения согласующего коэффициента пропорциональности?

3. При каком значении скорости вращения системы координат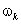 реальные переменные напряжения, приложенные к обмоткам статора, преобразуются в постоянное напряжение U_1max=const.

ОТВЕТЫ