Лекция No 12.

Тема: «Ранжирование математических моделей электромеханических систем»

Тип математической модели управляемого объекта оказывает существенное влияние на формирование структуры и параметров каждого множества тройки {I_q}, , {Opt I_q}, определяющей систему управления.

Причем элементы второго множества непосредственно представляют собой математические модели ; в элементах первого множества {I_q} математические модели для формирования функционала качества; выбор элементов третьего множества осуществляется в непосредственной зависимости от используемых математических моделей.

В подавляющем большинстве случаев для получения необходимой информации о свойствах реального объекта наблюдения необходима постановка серии экспериментов с его моделью (“прогона” модели). Поэтому, наибольший интерес представляют имитационные модели.

Следуя предложениям Р. Шеннона [12], имитационные модели удобно представлять в виде непрерывного спектра, простирающегося в общем случае от точных моделей или макетов реальных объектов до совершенно абстрактных символических моделей (рис. 12.1).

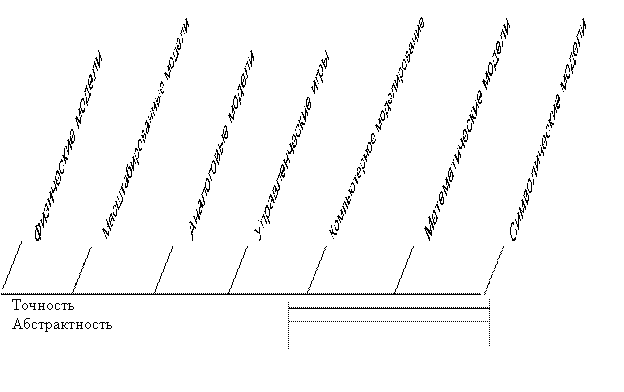
Рис. 12.1. Общий спектр имитационных моделей.

Очевидно, что использование полного спектра имитационных моделей практически невозможно, т.к. сопряжено с неоправданными затратами. На этапе автоматизации функционального проектирования ЭМС целесообразно использовать модели, которые могут быть реализованы на ЭВМ. В общем спектре (рис. 12.1) они расположены в правой части спектра.

В задачах функционального проектирования, реальный объект представляется динамической системой с точки зрения ее внешнего поведения, которую можно рассматривать как абстрактный набор упорядоченных данных о входных воздействиях U(t) и наблюдаемых выходных координатах Y(t).

В реальной ситуации конечной паре множеств {U, Y} можно поставить в соответствие бесконечное множество моделей.

Необходимость создания элементов технологии рационального применения имитационных моделей ЭМС в задачах их функционального проектирования потребовала формирования спектра этих моделей, в котором последние должны располагаться:

• по мере снижения точности или адекватности динамических процессов (шкала точности);

• по мере снижения сложности описания структуры и параметров, используемого математического аппарата и численных методов (шкала сложности);

• по мере увеличения абстрактности внешнего представления (шкала формализации);

• по мере снижения сложности компьютерной реализации (шкала реализации);

• по мере снижения времени “прогона” модели (шкала быстродействия).

Кроме того, несомненный интерес представляют факторы, характеризующие простоту машинной реализации модели, наглядность, простоту, доступность, связь с физической реальностью модели для пользователя.

Для динамических систем взаимная связь между множеством входных воздействий U(t) и выходных координат Y(t) описывается с помощью нелинейных непрерывно-дискретных дифференциальных, алгебраических, логических уравнений постоянной и переменной структуры. К настоящему времени чаще всего используют два вида описаний:

• - описание в терминах “вход-выход”;

• - описание в терминах “пространства состояний”.

Базовым инструментом описания первого вида является структурная модель, понятие которой определено в первой части курса.

Структурная модель - некоторая схема из взаимосвязанных элементов, выделяемых по физическому назначению или выполняемой математической функции.

На математическом уровне, который является базовым для пользователя, структурная модель представляет собой совокупность блоков уравнений, которые выполняются по функциональному или физическому принципу, что позволяет легко формировать модели, близкие по структуре реальной технической системе. Графическое представление структурных моделей на этом уровне в определенном смысле соответствует традиционной структурной схеме с значительно расширенном составом динамических элементов.

Динамические элементы призваны осуществлять такие функции, как:

• безынерционные преобразования сигналов (суммирование, усиление, уменьшение, деление);

• интегрирование сигналов;

• разнообразные нелинейные операции;

• сложные логические операции;

• вычисления таблично заданных функций;

• операции дискретизации непрерывных сигналов, генерации дискретных событий;

• преобразования дискретных сигналов;

• прием и обработка сигналов с реального объекта.

Кроме того, для обеспечения корректной имитации алгоритмов управления и систем переменной структуры используются алгоритмические элементы. Алгоритмический элемент выполняет определенную последовательность действий (алгоритм). Однако, результаты вычислений присваиваются переменным, элементам массивов, выходам динамических элементов, которые не имеют строгой привязки к конкретным элементам, То есть, любой алгоритмический элемент может изменять значение любой переменной. Кроме того, алгоритмические элементы осуществляют оперативную корректировку плана вычислительного процесса при изменении структуры модели с помощью средств активизации динамических элементов.

Таким образом, с помощью расширенного состава динамических и алгоритмических элементов могут быть построены структурные модели широкого класса ЭМС. При этом достигается максимальная точность воспроизведения динамических процессов.

Для определения упорядоченных по введенным выше шкалам последовательностей структурных моделей, последние могут быть условно разделены на следующие виды:

• линейные непрерывные модели, т.е. модели, построенные на базе линейных непрерывных дифференциальных уравнений, коэффициентов передачи и передающих функций элементов (для кратности представления будем называть такие модели L - модели);

• - нелинейные непрерывные модели - модели, построенные на базе нелинейных непрерывных дифференциальных уравнений (N - модели);

• нелинейные непрерывно-дискретные модели - модели, обеспечивающие при сохранении всех свойств N - моделей имитацию динамического поведения системы при непрерывных и дискретных сигналах управления (ND - модели);

• нелинейные, непрерывно-дискретные нестационарные модели - модели, обеспечивающие при сохранении всех свойств ND - моделей корректную имитацию систем переменной структуры и управляющих алгоритмов (NVS - модели);

• физико-математические модели - модели, обеспечивающие при сохранении свойств моделей предыдущих видов включения в свою структуру реальных элементов ЭМС и имитацию процессов в режиме реального времени (FM - модели).

В последние годы в теории автоматического управления (ТАУ), являющейся фундаментальной теоретической основой функционального проектирования ЭМС, в ряде других областей применения теории систем отмечается очень сильное развитие методов пространства состояний.

Базовым инструментом описания динамических систем в терминах “пространства состояний” является векторно-матричная модель (ВММ).

Основываясь на понятии состояния системы, приведенном в лекции 10, можно утверждать, что динамическая система может быть описана парой матричных уравнений

где

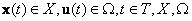
- множества состояний и входных воздействий, Т - упорядоченное множество моментов времени.

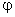- n-мерная вектор-функция системы, 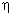- m-мерная вектор-функция выхода. Причем n - соответствует размерности пространства состояний и, следовательно, размерности вектора состояний x(t), m - соответствует числу входов системы и, следовательно, размерности вектора выхода y(t). Число выходов системы r соответствует размерности вектора входа u(t).

Матричное уравнение (12.1) называют уравнением состояния системы, а матричное уравнение (12.2) - уравнением выхода.

Если множество Х принадлежит конечномерному пространству, то (12.1) представляет собой конечномерную систему нелинейных нестационарных дифференциальных уравнений. Из системы (12.1) при определенных предположениях могут быть получены системы линейных и (или) стационарных уравнений, дискретная система (также линейная и (или) стационарная).

Чем уже область определения

,

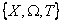тем ближе в пространстве Х будет упрощенная модель к исходной (12.1).

В частном случае вектор-функции

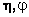
могут быть линейными комбинациями переменных состояния х_i, и выходных переменных U_q. При этом динамическая система описывается в векторно-матричной форме

В то же время для гладкой системы (12.3) - (12.4) следует существование таких

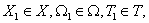
что с точностью до 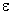системе (12.1) - (12.2) будет эквивалентна система дифференциальных уравнений с постоянными матрицами коэффициентов:

где А, B, C, D - матрицы размера (n x n), (n x r), (m x n),(m x r) соответственно.

Таким образом, модель (12.5)- (12.6) описывает динамическое поведение системы в классе линейных непрерывных стационарных систем и с точки зрения математического описания процессов полностью соответствует структурной линейной непрерывной модели (L - модели).

Назовем модель (12.5)- (12.6) линейной векторно-матричной моделью в непрерывном времени (VML -моделью). Отметим, что ВММ имеет единую форму представления независимо от размерности, что значительно облегчает алгоритмизацию и компьютерную реализацию в исследовательских и проектных операциях, а также предоставляет возможность исследования новых свойств объектов управления, которые скрыты при использовании структурных моделей (управляемость, наблюдаемость).

Из недостатков ВММ, прежде всего, следует отметить:

Широкое применение в теории и в практике автоматического управления цифровых управляющих устройств и систем управления с ЭВМ, обусловливает необходимость построения ВММ непрерывных объектов в дискретном времени.

Цифровые системы управления содержат как непрерывные, так и квантованные или дискретные сигналы. Наличие сигналов различного типа затрудняет описание динамического поведения системы. Однако часто можно ограничиться описанием поведения системы в моменты квантования. Такие системы называют системами дискретного времени, они оперируют с последовательностями чисел и, следовательно, для их описания естественно использовать разностные уравнения.

Проблема заключается в нахождении способа описания непрерывной динамической системы, связанной с ЭВМ посредством аналого-цифрового (АЦП) и цифро-аналогового преобразователей (ЦАП). Наиболее распространена ситуация, когда АЦП сохраняет уровень аналогового сигнала до тех пор, пока не потребуется новое преобразование.

Характеристики системы между моментами квантования дают в этом случае представление о реакции системы на ступенчатое воздействие с начальными условиями, т.е. между моментами квантования система функционирует как разомкнутая. Для периодического квантования с периодом Т модель сводится к системе разностных уравнений, которая при Т=1 (принимается только для простоты записи) имеет вид:

где

Назовем ВММ непрерывного объекта (12.5) - (12.6) в дискретном времени, представленную в форме уравнений (12.7) - (12.8) линейной векторно-матричной моделью в дискретном времени (VLD- моделью).

Таким образом, для получения VLD- модели требуется вычислить матричную экспоненту и проинтегрировать ее.

Применение в задачах функционального проектирования ВММ вида (12.5) - (12.6) для нелинейных объектов может привести к существенным ошибкам. Однако, отмеченные преимущества таких моделей обусловливают насущную необходимость их совершенствования в направлении учета нелинейных функций отдельных элементов.

Для построения VML- модели вида (12.5) - (12.6) по известной модели динамической системы общего вида (12.1) - (12.2) необходимо вычисление матриц Якоби

в точке (х^?, u^?, t)

Для достижения максимального соответствия динамических процессов, полученных при использовании моделей (12.1) - (12.2) и (12.5) - (12.6) можно найти как в направлении поиска оптимальной точки линеаризации (х^?, u^?, t), так и в направлении применения пошаговой линеаризации (12.10)в соответствии с изменением векторов состояния и управления х(t) и u(t). Последнее соответствует использованию конечного множества точек линеаризации {L₁, L₂,...L_q}, где L_j=(x_j, u_j, t).

В этом случае получается q - VML- моделей, которые могут быть идентифицированы одной нелинейной векторно-матричной моделью в непрерывном времени (VNN-моделью) путем применения трехмерных матриц A_N, B_N, размером (n x n x q) и (n x m x q) соответственно.

Необходимость изучения процессов в дискретном времени требует решения задач конструирования и применения нелинейных векторно-матричных моделей в дискретном времени (VND - моделей), которые используют трехмерные матрицы Ф_N, Г_N, размером (n x n x q) и (n x m x q) соответственно (здесь q - число точек линеаризации).

Расположить каждый вид имитационной модели на предложенных выше шкалах, очевидно, можно лишь условно. Это объясняется тем, что практически невозможно каждому виду модели сопоставить определенное значение показателя i - ой шкалы.

Однако, качественная оценка месторасположения каждого вида имитационных моделей на каждой из предложенных шкал представляет несомненный интерес.

Предварительно определим способы оценки показателей шкал для конкретной имитационной модели.

Теоретически численные значения точности модели может определяться через показатель отклонения “истинного” поведения исследуемой системы от результатов “прогона” имитационной модели.

Логично в качестве “истинного” поведения исследуемой системы принимать результаты “прогонов” имитационной модели, построенной на основании имеющегося опыта моделирования родственных систем и информации, имеющейся в базе моделей, базе знаний и базе данных инструментального программно-технического комплекса исследования и проектирования ЭМС.

Если ввести вектор отклонения наблюдаемых координат “истинного” поведения системы

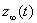
от соответствующих координат модели z_m (t)

то показатель отклонения можно определить следующим образом

где F, Q - постоянные диагональные матрицы весовых коэффициентов, t₁, t_k - соответственно начальное и конечное значение времени наблюдения.

Так как получить истинную модель в смысле абсолютно точного воспроизведения всех динамических процессов

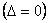
практически невозможно, то показателем точности будем считать величину обратную показателю отклонения, т.е.

Очевидно, что наивысший показатель сложности Р_T может быть получен при использовании физико-математических моделей. Но так как их использование ограничено определенными техническими трудностями реализации и необходимостью обеспечения режима реального времени, наибольший интерес представляют все-таки чисто программные модели, качественное распределение которых по шкале точности приведено на рис. 12.2.

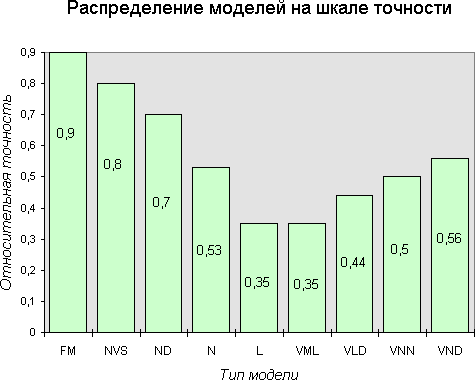
Рис. 12.2. Шкала точности

Вслед за FM- моделями располагаются NVS-модели. Так как NVS- модели позволяют имитировать подавляющее большинство динамических и алгоритмических свойств ЭМС.

Минимальные показатели точности имеют L и VML- модели, т.к. описание в классе непрерывных линейных дифференциальных уравнений является самым приближенным.

Для оценки сложности структурных моделей всех видов будем использовать так называемую топологическую сложность, которая определяется суммой порядков передаточных функций каждого базового элемента структурной модели математического уровня и суммарной сложностью элементов каждого класса, кроме линейных инерционных элементов.

где N_S - общее число элементов структурной модели математического уровня; m_i, n_i - порядок числителя и знаменателя i-го элемента; r - число классов используемых элементов (нелинейные, специальные, алгоритмические и т. п.), N_r - число элементов каждого класса, C_jk - сложность k-го элемента j-го класса.

Определение сложности C_jk элементов каждого класса не поддается формализации. Поэтому, она определяется интуитивно в процессе создания и эксплуатации программно-технического комплекса имитационного моделирования и функционального проектирования ЭМС.

Сложность векторно-матричной модели С_ВММ будем оценивать как

где n - число переменных состояния ВММ, m - число входных переменных, l - число точек линеаризации для VNN и VND- моделей.

Качественное расположение структурных и векторно-матричных моделей по шкале сложности, основанное на выражениях (12.19)- (12.19)приведено на рис. 12.3.

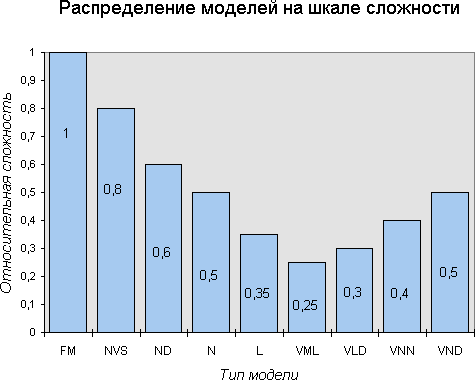
Рис. 12.3 Шкала сложности

Концепция структурного моделирования, представленная в первой части курса, предусматривает использование единого внешнего представления структурных моделей в виде функциональных блоков, выделяемых преимущественно по физическому назначению. Аппарат вложенных функциональных блоков позволяет представить структурную модель в виде, максимально соответствующем функциональной схеме ЭМС. Поэтому по степени формализации внешнего представления структурные модели всех видов неразличимы, т.к. ориентированы, прежде всего, на пользователя, а не на ЭВМ.

Векторно-матричные модели, базирующиеся на теории пространства состояний, имеют достаточно высокий показатель формализации и являются наиболее приемлемыми для реализации на ЭВМ. С учетом вышеизложенного качественное расположение моделей на шкале формализации приведено на рис. 12.4.

Рис 12.4 Шкала формализации

Наименьшие затраты компьютерной реализации модели требуется при представлении последней в виде модели алгоритмического уровня, т.е. в виде некоторой схемы, элементы которой используются непосредственно для планирования вычислительного процесса. Высокий уровень формализации ВММ значительно приближает их к моделям алгоритмического уровня. Поэтому, наименьшую сложность компьютерной реализации имеют VML, VLD- модели. Некоторое увеличение сложности реализации наблюдается для VNN и VND- моделей, которое объясняется необходимостью обработки переменной структуры этих моделей.

Качественное расположение моделей на шкале реализации приведено на рис. 12.5

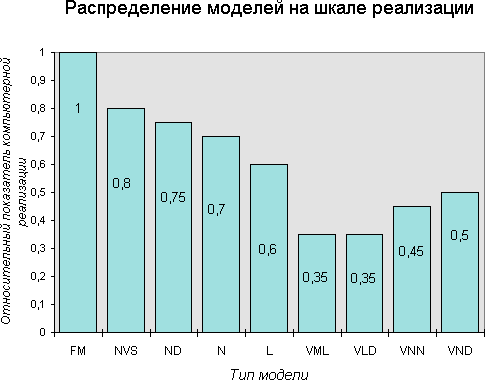
Рис. 12.5 Шкала реализации

Быстродействие конкретной модели в значительной мере определяется быстродействием используемой ЭВМ и быстродействием применяемых методов численного интегрирования дифференциальных уравнений. Но, так как эти составляющие для конкретных ЭВМ и методов численного интегрирования неизменны, их можно не учитывать при разложении моделей на шкале быстродействия.

Действительная оценка времени “прогона” любого вида имитационной модели может быть получена на основании статистических сведений о задачах. Для этого введено понятие эффективного быстродействия, под которым понимается математическое ожидание отношения сложности задач к математическому ожиданию времени решения этих задач

где С - сложность модели, Р(с) - плотность распределения вероятности появления задачи сложности С, t_C - математическое ожидание времени “прогона” модели сложности С.

Анализ выражения (12.20)показывает, что время “прогона” конкретного вида модели в определенной степени пропорционален сложности этой модели.

Если в качестве показателя быстродействия принять величину, обратную времени “прогона” модели, качественное расположение моделей на шкале быстродействия принимает вид, представленный на рис. 12.6.

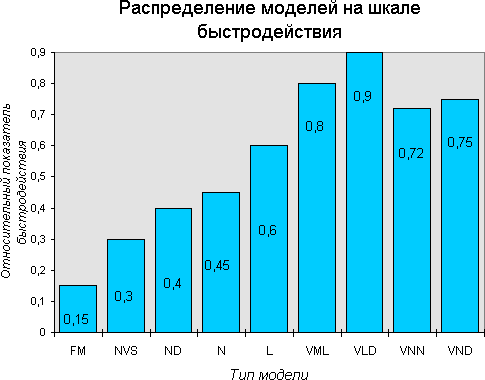
Рис. 12.6 Шкала относительного быстродействия

Контрольные вопросы к лекции No 12.

1. Дайте общее определение структурной модели. Определите структурные модели математического уровня.

2. Какие модели называют линейными непрерывными моделями (L – моделями)?

3. Какие модели называют нелинейными непрерывными моделями (N – моделями)?

4. Какие модели называют нелинейными непрерывно-дискретными моделями ((ND -– моделями)?

5. Какие модели называют нелинейными непрерывно-дискретными нестационарными моделями ((NVS – моделями)?

6. Какие модели называют физико-математическими моделями ((FM - моделями)?

7. Какие модели называют линейными векторно-матричными моделями в непрерывном времени (VML -моделями)?

8. Какие модели называют линейными векторно-матричными моделями в дискретном времени (VNN -моделями)?

9. Какие модели называют нелинейными векторно-матричными моделями в непрерывном времени (VLD -моделями)?

10. Какие модели называют нелинейными векторно-матричными моделями в дискретном времени (VND -моделями)?

11. Шкалы каких показателей предлагается использовать при ранжировании математических моделей электромеханических систем?

12. Какие виды моделей имеют наименьшие значения показателя точности?

13. Какие виды моделей имеют наибольшие значения показателя сложности?

14. Какие виды моделей имеют наибольшие значения показателя формализации?

15. Какие виды моделей имеют наименьшие значения показателя реализации?

16. Какие виды моделей имеют наибольшие значения показателя быстродействия?

ОТВЕТЫ