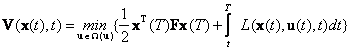
(П.2.1)
Вывод уравнения Риккати
Решим уравнение Беллмана (9.3) для объекта управления (9.1) и функционала качества (9.2).
Наличие неинтегрального члена в составе функционала (9.2) не влияет на структуру уравнения Беллмана, если принять
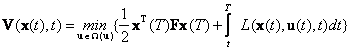 |
(П.2.1) |
где L - подынтегральная функция из (9.2).
Тогда уравнение Беллмана принимает вид
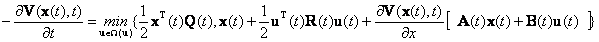 |
(П.2.2) |
Оптимальное уравнение будем искать из условия
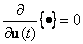
Выполнив дифференцирование, получим
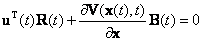 |
(П.2.3) |
Из (П.2.3) получаем оптимальное уравнение
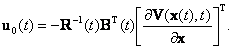 |
(П.2.4) |
Чтобы использовать выражение (П.2.4), необходимо найти функцию V(x(t),t). Для этого подставим (П.2.4) в (П.2.2):
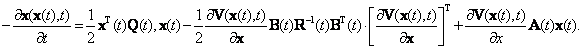 |
(П.2.5) |
Решение (П.2.5) при t=T должно удовлетворять условию
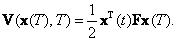 |
(П.2.6) |
Общее решение будем искать в виде квадратной формы переменных состояния
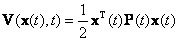 |
(П.2.7) |
где P(t)=PT(t) - неизвестная симметричная нестационарная n x n-матрица.
Подставим в (П.2.5) выражение (П.2.7) и
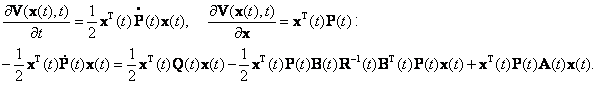
Последнее слагаемое представим суммой

Тогда полученное соотношение преобразуется к виду
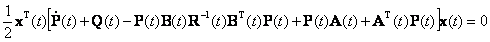
При любых состояниях x(t)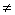 0 предыдущее соотношение выполняется, если
0 предыдущее соотношение выполняется, если
 |
(П.2.8) |
В результате получили нелинейное дифференциальное уравнение, известное под названием матричного уравнения Риккати.
Очевидно, что его решение следует искать при граничном условии
|
P(T)=F |
(П.2.9) |
Для стационарных систем уравнение (П.2.8) становится алгебраическим:
 |
(П.2.10) |