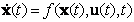
(П.1.1)
Вывод уравнения Беллмана
Пусть управляемый объект описывается векторным дифференциальным уравнением общего вида
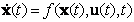 |
(П.1.1) |
а критерий оптимальности также имеет общий вид
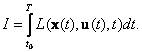 |
(П.1.2) |
Необходимо в классе допустимых управлений найти управление u0(t), при котором функционал I достигает минимального значения, т.е.
 |
(П.1.3) |
а объект переводится за время T- t0 из заданного начального состояния x(t0) в произвольное конечное, принадлежащее пространству состояний.
В основу дальнейших рассуждений положен принцип оптимальности, утверждающий, что любой оставшийся конечный участок оптимальной траектории сам по себе является также оптимальной траекторией.
Предположим, что уже найдены оптимальное управление u0(t) и соответствующая ему траектория движения объекта x(t). Выберем на оптимальной траектории две точки, соответствующие моментам времени t и t+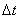 , где
, где 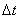 - малая величина. Согласно принципу оптимальности участки оптимальной траектории от точек t и t+
- малая величина. Согласно принципу оптимальности участки оптимальной траектории от точек t и t+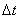 до конечной точки Т являются оптимальными. Обозначим минимальное значение функционала (П.1.2), соответствующее этим участкам:
до конечной точки Т являются оптимальными. Обозначим минимальное значение функционала (П.1.2), соответствующее этим участкам:
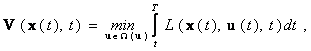 |
(П.1.4) |
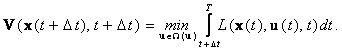 |
(П.1.5) |
На основании выражений (П.1.4), (П.1.5) можно записать
 |
(П.1.6) |
Учитывая малость 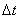 , запишем
, запишем
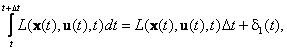 |
(П.1.7) |
где  - малая с большим порядком малости, чем
- малая с большим порядком малости, чем 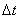 .
.
Функцию х(t+ ) разложим в ряд Тейлора в окрестности точки t, представив его в виде
 |
(П.1.8) |
где  - совокупность последующих членов ряда.
- совокупность последующих членов ряда.
Предполагая дифференцируемость функции V по своим аргументами и учитывая (П.1.8), функцию V(x(t+ ), t+ ) разложим в ряд Тейлора в окрестности точки (x(t), t):
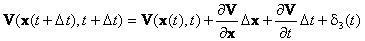 |
(П.1.9) |
где 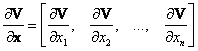 - вектор-строка частных производных в точке (x(t),t);
- вектор-строка частных производных в точке (x(t),t);  - приращение вектора x(t);
- приращение вектора x(t); 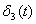 - совокупность последующих членов ряда Тейлора.
- совокупность последующих членов ряда Тейлора.
Подставим (П.1.7), (П.1.9) в (П.1.6):
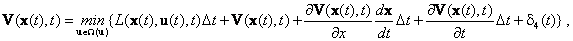 |
(П.1.10) |
где 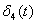 - все члены с порядком малости, большим, чем у
- все члены с порядком малости, большим, чем у 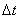 .
.
Так как величина V(x(t),t) не зависит от управления, вынесем ее из-под символа минимума и взаимно уничтожим с левой частью выражения. Оставшиеся члены разделим на 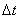 . Производную
. Производную 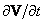 , не зависящую от u(t), вынесем за скобки, а производную
, не зависящую от u(t), вынесем за скобки, а производную  заменим согласно (П.1.1) функцией f. Тогда с учетом того, что
заменим согласно (П.1.1) функцией f. Тогда с учетом того, что 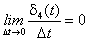 , получим уравнение Беллмана
, получим уравнение Беллмана
 |
(П.1.11) |