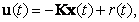
(8.1)
Тема: «Принципы детерминированного синтеза систем управления»
Понятие “синтез” означает нахождение такой структуры и параметров системы управления, при которых выходные переменные объекта управления (ОУ) отвечают задан-ным требованиям или критериям качества. Решение проблем автоматизации процедуры син-теза систем управления (СУ) сопряжено с построением универсальных алгоритмов, обеспе-чивающих поиск оптимальных структуры и параметров СУ, не зависимо от сложности ОУ.
Очевидно, что универсальность алгоритмов и их инвариантность к сложности ОУ может быть достигнута только при использовании высокоформализованных упрощенных математических моделей ОУ, которыми являются векторно-матричные модели.
Если синтез осуществляется в пространстве состояний, то при известном состоянии x(t1) в момент времени t1 должна существовать возможность нахождения такого управления, которое будет удовлетворять требованиям, налагаемым на выход объекта. Эти требования формируются с помощью критериев качества управления, которые рассмотрены в предыду-щем разделе.
В большинстве практических задачах синтеза СУ возникает противоречивая ситуа-ция: объект управления обладает нелинейными свойствами, устройства управления предпо-лагается реализовать с помощью средств цифровой (микропроцессорной) техники, а наибо-лее простыми, доступными и эффективными являются алгоритмы и программы синтеза СУ с помощью линейных непрерывных моделей.
В том случае, когда ВММ удовлетворяет требованиям адекватности описания нели-нейного ОУ и требованиям представления дискретного управляющего устройства примене-ние указанных алгоритмов вполне оправдано и наиболее рационально. Однако и при невы-полнении этих требований выполнение процедуры синтеза СУ целесообразно начать с ис-пользования ВММ с последующим их усложнением до требуемого вида. Таким образом, не-смотря на техническую сложность современных ЭМС, нелинейные свойства ОУ и дискрет-ный характер управления, алгоритмы синтеза и анализа СУ, основанные на матричных опе-рациях с векторно-матричными моделями, не потеряли свою актуальность.
Этап функционального проектирования систем управления предусматривает выпол-нение следующих проектных операций:
В линейном случае мы всегда выражаем вектор входа через линейную комбинацию компонент вектора состояния, т.е. в непрерывном времени с помощью уравнения
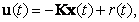 |
(8.1) |
а в дискретном случае с помощью уравнения
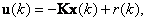 |
(8.2) |
где r(t), r(k) - задающая переменная.
Следует отметить, что уравнения (8.1), (8.2) имеют вид уравнений выхода векторно-матричной модели в пространстве состояний и, таким образом, управляющее устройство, определяемое уравнениями (8.1), (8.2), является статическим. Требуемый астатизм обес-печивается дополнительным включением в СУ элементов, обладающих интегрирующими свойствами.
Для решения задачи синтеза в такой постановке, необходимо измерение всех компо-нент вектора состояния объекта x(t). Если состояние объекта неизмеряемо, его надо оценить. В детерминированных системах это осуществляется с помощью наблюдателя. Сначала оце-нивается вектор состояния 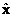 (t), а затем рассчитывается вектор входа объекта
(t), а затем рассчитывается вектор входа объекта
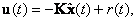 |
(8.3) |
Одним из фундаментальных методов проектирования детерминированных систем управления в пространстве состояний является метод расположения полюсов.
Как было отмечено в разделе. 3, в линейных системах качество управления и динами-ческие показатели системы можно задать с помощью корней характеристического уравнения или полинома замкнутой системы.
Общая постановка задачи. Для стационарного непрерывного управляемого объекта, уравнение динамики которого имеет вид
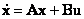 |
(8.4) |
и управляющего устройства, описываемого уравнением
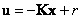 |
(8.5) |
необходимо определить матрицу К, такую, чтобы замкнутая система, получаемая подстанов-кой (8.5) в (8.4),
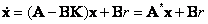 |
(8.6) |
имела желаемый характеристический полином
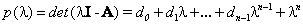 |
(8.7) |
Общая схема системы управления будет иметь вид, представленный в среде компью-терного комплекса FuncPro 1.0 на рис 8.1.
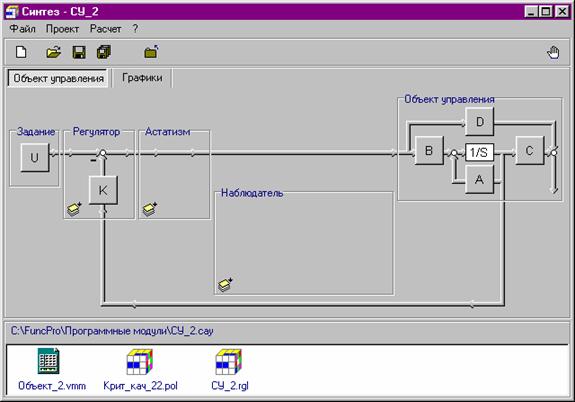
Рис. 8.1. Схема системы управления с регулятором состояния
Методические аспекты выбора желаемого полинома (8.7) подробно изложены в лек-ции 6.. Здесь же рассмотрим ряд алгоритмов вычисления матрицы коэффициентов обратных связей К.
Алгоритм 1. Рассмотрим управляемый объект с одним входом и одним выходом. Подстановкой
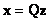 |
(8.8) |
преобразуем его к канонической форме управляемости
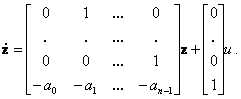 |
(8.9) |
Для линейных стационарных систем характер свободного движения не изменится, ес-ли выбрать вместо (8.5) регулятор вида
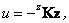 |
(8.10) |
или
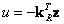 , где
, где 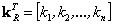 .
.
Подставляя (8.10) в (8.9), получим
 |
(8.11) |
В этом случае характеристический полином имеет вид
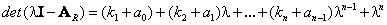 |
(8.12) |
Сопоставляя полиномы (8.12) и (8.7), получаем соотношения для вычисления коэф-фициентов матрицы регулятора kRT:
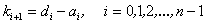 |
(8.13) |
Связь между управляющей переменной u и вектором состояния х определяется со-гласно выражению (8.10):
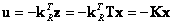 |
(8.14) |
то есть
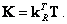 |
(8.15) |
Из этого следует, что для вычисления коэффициентов обратных связей нужно опреде-лить еще и матрицу преобразования 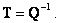
Таким образом, алгоритм 1 синтеза регулятора состояния может быть сформулирован следующим образом:
1. На основании требований технического задания к динамическим характеристикам проектируемой СУ формируется критерий качества управления в форме характеристического полинома (8.13), т.е. определяются коэффициенты d0, d1, d2, ..., dn-1.
2. Векторно-матричная модель объекта преобразуется к канонической форме управляемо-сти. В процессе преобразования определяются коэффициенты характеристического урав-нения a0 , a1 , a2 , ..., an-1 , прямая и обратная матрицы преобразования 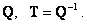
3. На основании выражения (8.13) вычисляются коэффициенты матрицы 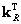 .
.
4. По формуле (8.15) определяется матрица реальных коэффициентов обратных связей К по полному вектору состояния.
Алгоритм 2. Общность постановки задачи не нарушится, если считать, что оптималь-ные динамические характеристики проектируемой системы задаются в виде эталонной моде-ли
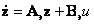 |
(8.16) |
имеющей тот же порядок, что и модель объекта (8.4).
Тогда коэффициенты регулятора состояния однозначно определятся путем решения уравнения
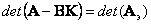 |
(8.17) |
Процесс синтеза сводится к двум задачам:
1) определение эталонной модели (8.16);
2) решение уравнения (8.17).
Наиболее просто желаемое качество управления можно задать с помощью эталонной модели, представленной в канонической форме управляемости
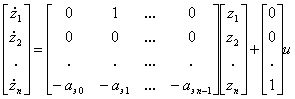 |
(8.18) |
Коэффициенты аэ0, аэ1, ... , аэ n-1 в этом случае соответствуют коэффициентам d0, d1, ..., dn-1 желаемого характеристического полинома (8.7).
Для согласования объекта и эталонной модели введем линейное преобразование
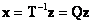 |
(8.19) |
После преобразования (8.9) система “объект + регулятор” (8.6) относительно нового базиса имеет вид
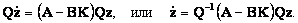
Из условия равенства собственных движений синтезируемой системы и эталонной модели следует, что 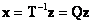 .
.
Откуда получается выражение для вычисления значений матрицы обратных связей К регулятора состояния:
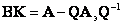 |
(8.20) |
Таким образом, для синтеза регулятора состояния в этом случае необходимо:
Алгоритм 3. Если матрица входов В ВММ объекта управления имеет больше одного ненулевого элемента, то применение алгоритма 2 вызывает определенные затруднения. Для их устранения используем следующую методику.
Представим эталонную матрицу как сумму двух матриц:
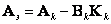 |
(8.21) |
где 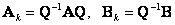 - коэффициентные матрицы объекта управления в канониче-ской форме управляемости; Кk - матрица коэффициентов обратных связей в канонической форме.
- коэффициентные матрицы объекта управления в канониче-ской форме управляемости; Кk - матрица коэффициентов обратных связей в канонической форме.
Подставляя (8.21) в (8.20):
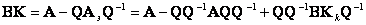
получим
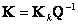 |
(8.22) |
Так как 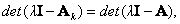 то согласно (8.21) элементы матрицы Кk можно опреде-лить из уравнения
то согласно (8.21) элементы матрицы Кk можно опреде-лить из уравнения
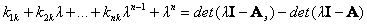 |
(8.23) |
Итак, алгоритм 3 формируется как последовательность следующих операций:
1. Вычисление матриц преобразования ОУ к канонической форме управляемости Q и Q-1.
2. Решение уравнения (8.23) относительно Кk.
3. Вычисление реальных коэффициентов обратных связей (матрицы К) по формуле (8.22).
Сравнительно высокая сложность приведенных выше алгоритмов делает практически неосуществимыми проектные операции синтеза регулятора состояния без ЭВМ.
Компьютерная реализация представленных выше алгоритмов синтеза регулятора со-стояния при построенной ВММ ОУ затруднений не вызывает, так как все вычисления по-строены на основе типовых операций обработки матриц и матричной алгебры.
Эффективность проектных решений, полученных в результате вычислительных экс-периментов, выполняемых с помощью компьютерных средств реализации указанных алго-ритмов, может быть повышена за счет включения пользователя в заключительный этап уточнения параметров регулятора состояния (РС).
В практических ситуациях часто нет необходимости использовать в дальнейших опе-рациях точные значения расчетных параметров РС. Это объясняется возможными погрешно-стями и трудностями реализации. Поэтому вполне оправдано уже на начальных стадиях про-ектирования "поиграть" параметрами РС и дополнительных устройств, а в отдельных случа-ях даже сократить число обратных связей СУ.
Пример 8.1. Для упругого электромеханического объекта, который подробно пред-ставлен в лекции 1, синтезируем регулятор состояния.
При построении ВММ откажемся от учета инерционности преобразователя и введем следующие компоненты вектора состояния 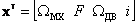 , где
, где 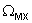 - скорость враще-ния платформы, F- усилие, под действие которого вращается платформа,
- скорость враще-ния платформы, F- усилие, под действие которого вращается платформа, 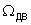 - скорость вращения электродвигателя, i - ток электродвигателя.
- скорость вращения электродвигателя, i - ток электродвигателя.
Таблица 8.1. Параметры электромеханического объекта

Векторно-матричная модель объекта с учетом численных значений параметров пре-образователя, электродвигателя и механизма, приведенных в табл. 8.1., принимает следую-щий вид:

Желаемые динамические показатели управления были определены с помощью инст-рументальных средств формирования критерия качества путем некоторой модификации стандартного распределения Баттерворта для среднегеометрического корня 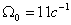 . В ре-зультате был выбран желаемый характеристический полином
. В ре-зультате был выбран желаемый характеристический полином
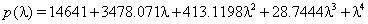
которому соответствует эталонная модель, представленная в канонической форме

Вычислительные эксперименты, выполненные с помощью компьютерного комплекса функционального проектирования СУ, позволили получить расчетные параметры регулятора состояния в виде значений коэффициентов обратных связей по вектору состояния, которые приведены во второй строке табл. 8.2.
Таблица 8.2. Параметры регулятора состояния

Анализ полученных результатов показывает, что для обеспечения заданного качества динамических характеристик СУ электромеханическим объектом необходимо введение сла-бой положительной обратной связи по току электродвигателя, что нежелательно. В этой свя-зи было принято решение в дальнейшем отказаться от реализации обратной связи по току, а значения других коэффициентов округлить в допустимых пределах. Выбранные значения параметров дальнейшей реализации регулятора состояния приведены в третьей строке табл. 8.2.
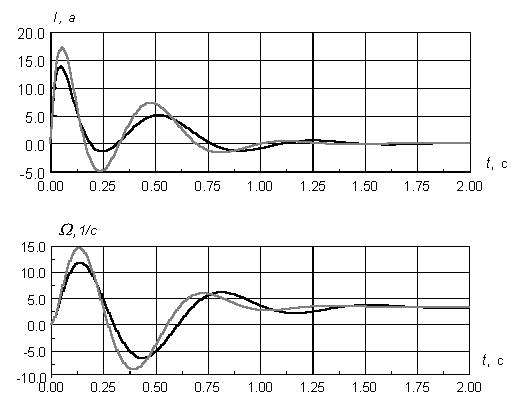
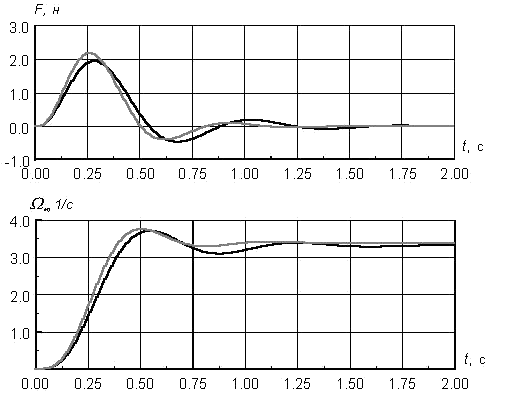
Обоснованность принятого решения доказывают приведенные на рис. 8.2 предвари-тельные результаты вычислительных экспериментов с моделями синтезированных систем управления. Суммарное среднеквадратичное отклонения выходной координаты не превыша-ет здесь 1.5%.
 - расчетные параметры регулятора состояния
- расчетные параметры регулятора состояния
 - параметры реализации
- параметры реализации
Рис. 8.2. Сравнительные динамические характеристики СУ
1. Для объекта, описанного ВММ, матрицы которой имеют размеры А(7x7), В(7x1), С(1x7), синтезирован регулятор состояния при допущении, что все переменные со-стояния измеряемы. Каков будет размер матрицы состояния системы «объект – регу-лятор»?
2. Какие операции должны быть обязательно выполнены при реализации любого из ал-горитмов синтеза регулятора состояния?
3. Каковы будут значения параметров регулятора состояния, синтезированного для объ-екта? Векторно-матричная модель объекта и эталонная модель системы управления приведены ниже.
1. ВММ объекта управления |
2. Эталонная модель СУ |
3 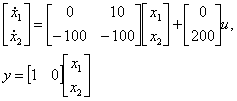 |
4 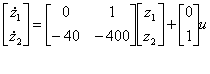 |
4. Каковы будут значения параметров регулятора состояния, синтезированного для объ-екта? Векторно-матричная модель объекта и эталонная модель системы управления приведены ниже.
5. ВММ объекта управления |
6. Эталонная модель СУ |
7 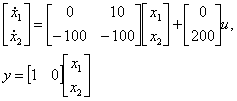 |
8 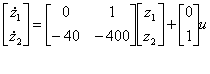 |
№ задания |
Ответ |
1 |
(7x7) |
2 |
a) оценка управляемости объекта; b) приведение векторно-матричной модели объекта управления к канонической форме управляемости; |
3 |
|
4 |
Не смогу рассчитать |