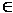 R1. Здесь R1
R1. Здесь R1 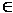 R, что соответствует выделению в пространстве состояний области допустимых состояний R и сужению ее до некоторой области R1, которая для нас по каким-то причинам является желательной.
R, что соответствует выделению в пространстве состояний области допустимых состояний R и сужению ее до некоторой области R1, которая для нас по каким-то причинам является желательной.Тема: «Критерии качества систем управления»
Процесс функционального проектирования систем управления неразрывно связан с решением задачи оптимизации управления, то есть задачи оптимального достижения главной цели при соблюдении множества ограничений. В общем случае цель управления заключается в том, чтобы перевести объект из начального состояния x(t0), в котором он находится в момент t0, в конечное состояние x(t2), принадлежащее подобласти R1 области допустимых состояний R , то есть x(t2) 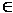 R1. Здесь R1
R1. Здесь R1 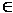 R, что соответствует выделению в пространстве состояний области допустимых состояний R и сужению ее до некоторой области R1, которая для нас по каким-то причинам является желательной.
R, что соответствует выделению в пространстве состояний области допустимых состояний R и сужению ее до некоторой области R1, которая для нас по каким-то причинам является желательной.
Задача управления заключается в том, чтобы в области допустимых управлений Q(u) найти такое управление, при котором будет достигнута цель.
Функционалы и функции, выражающие цель управления и ограничения, называют критериями качества.
Операция формирования критерия качества управления является наиболее ответственной на подготовительной стадии проектирования. Поэтому наиболее оптимальное ее выполнение достигается путем сочетания формализованных методов и творческой деятельности проектировщика, работающего в диалоге с вычислительной системой.
Рассмотрим некоторые методические аспекты формирования критериев качества управления для решения задач предварительного синтеза системы управления.
Качество управления можно описать двумя способами.
Первый способ предусматривает или непосредственное задание динамических характеристик выходных координат системы при типовых воздействиях, или задание совокупности прямых и косвенных показателей качества (значение перерегулирования, времени регулирования, статической ошибки, частоты среза, полосы пропускания и т.д.).
Второй способ основан на введении некоторого обобщенного функционала, определяемого всеми переменными системы управления u(t), x(t), y(t).
В теории линейных систем управления широко используются оба указанных способа.
При описании объекта управления с помощью векторно-матричной модели в пространстве состояний первый способ задания качества управления может быть трансформирован в оптимальное распределение на комплексной плоскости полюсов замкнутой системы.
Для системы, описываемой векторно-матричной моделью в непрерывном времени
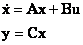 |
(6.1) |
полюса системы - это собственные значения матрицы А, которые обычно обозначаются через 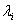 (A), где i=1, 2,..., n. В то же время собственными значениями матрицы А называются корни ее характеристического уравнения
(A), где i=1, 2,..., n. В то же время собственными значениями матрицы А называются корни ее характеристического уравнения
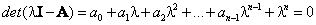 |
(6.2) |
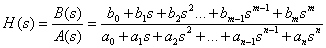 |
(6.3) |
полюса системы - это корни характеристического многочлена А(s). Соответственно нулями системы называются корни многочлена В(s), при которых Н(s)=0.
Расположение полюсов на комплексной плоскости во многом характеризует синтезируемую систему, определяя ее переходные и частотные характеристики, а, следовательно, и динамические показатели качества. Так, например, устойчивость системы определяется размещением полюсов в левой полуплоскости.
Наличие нулей в замкнутой системе в определенной степени влияет на ее динамику.
Синтезу регуляторов состояния предшествует решение задачи построения эталонной модели системы управления, которая соответствует желаемому распределению на комплексной плоскости корней характеристического уравнения A(s) = 0 замкнутой системы. Если все составляющие вектора состояния объекта могут быть измерены (имеется полная информация о векторе состояния), то обеспечение заданного расположения корней не вызывает трудностей. В этом случае возникает вопрос о том, какое расположение корней выбрать.
Если передаточная функция замкнутой системы не имеет нулей, то при выборе ее желаемого полинома A(s) можно руководствоваться стандартными формами (фильтрами), которые нашли достаточно широкое применение на практике. Стандартные формы определяют коэффициенты характеристического полинома (знаменателя) функции Н(s), обеспечивающие в системе переходные и частотные характеристики с известными показателями качества. Если же система характеризуется наличием нулей, стандартные формы могут служить в качестве исходного материала для поиска своего оптимального расположения корней. Как правило, в характеристическом полиноме сначала выделяются полюса для компенсации нулей, а оставшийся полином формируется из условия желаемого расположения корней.
В табл. 6.1 и 6.2 приводятся формулы характеристического полинома и соответствующие им коэффициенты для некоторых наиболее распространенных на практике распределений:/
Часто понятие оптимального переходного процесса связывают с минимизацией какого-либо функционала. Подобные стандартные формы получены эмпирически, и область их применения ограничивается системами невысокого порядка. К таким фильтрам относятся приведенные в табл. 6.3 распределения, минимизирующие интеграл от квадрата ошибки и оптимизирующий функционал.
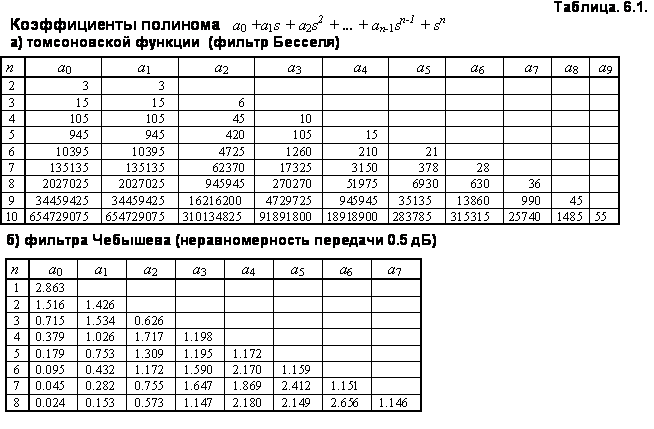

Качество работы системы управления характеризуется, с одной стороны, ее точностью в установившемся режиме, а c другой - переходным процессом от одного установившегося состояния к другому. При исследовании переходных процессов чаще всего полагают, что входной сигнал является единичной ступенчатой функцией. В этом случае кривая переходного процесса называется переходной функцией и характеризуется некоторыми показателями , принимаемыми за меру качества системы управления. К числу таких показателей могут быть отнесены (рис. 6.1):
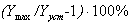 ;
;Перерегулирование и колебания - нежелательные свойства фильтра.
Типовые переходные характеристики для различных фильтров при входном ступенчатом сигнале качественно представлены на рис. 6.2.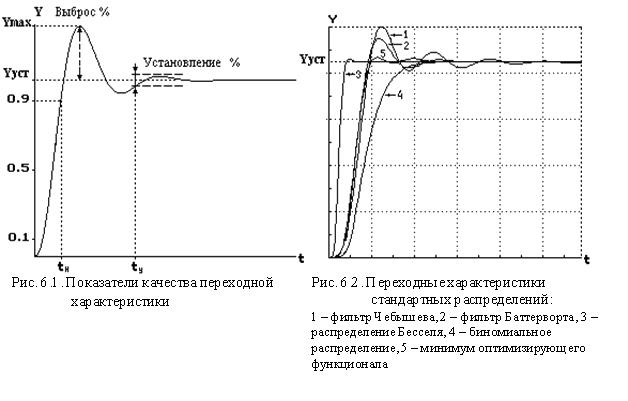
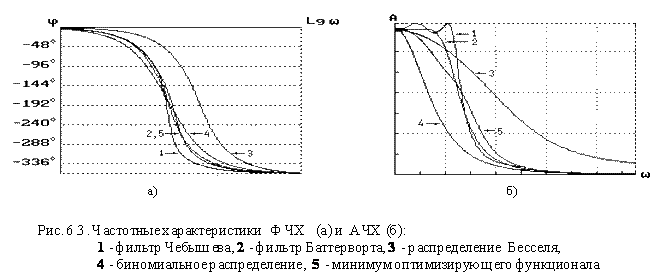
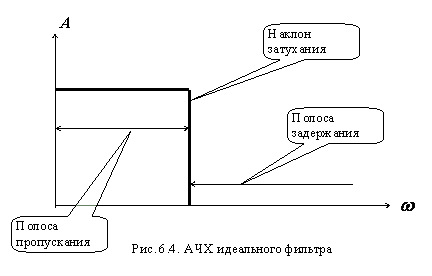
Как видно из рис. 6.3, наиболее полно сформулированным требованиям отвечает фильтр Баттерворта, имеющий максимально плоскую АЧХ в полосе пропускания и достаточно хорошую крутизну затухания. Распределение Чебышева используется в том случае, когда более важным параметром выступает крутизна нарастания затухания. Высокую скорость нарастания затухания обеспечивает отсутствие гладкой характеристики в полосе пропускания. Наихудшие показатели по АЧХ у фильтра Бесселя. Следует заметить, что при улучшении АЧХ фазочастотная характеристика ухудшается и наоборот. Поэтому между ними важно найти компромисс.
При синтезе системы управления среди частотных и временных характеристик предпочтение отдается последним, т.к. переходные кривые позволяют более наглядно представить поведение системы с учетом всестороннего влияния линейных и нелинейных внешних факторов. Сравнительная таблица примерных показателей качества переходных процессов для стандартных распределений (табл. 6.4) , а также рис. 6.2 дают наглядное представление о преимуществах или недостатках каждого из рассматриваемых здесь фильтров. Как видно, наилучшими показателями во временной области обладает фильтр Бесселя. Широкое распространение получили также распределение Баттерворта и распределение, минимизирующее оптимизирующий функционал. В любом случае к выбору расположения корней следует подходить исходя из конкретных целей и задач и с учетом свойств объекта проектирования.

1. Объект управления первоначально представлен передаточной функций
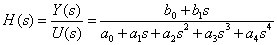
Какое число корней Вы должны расположить на комплексной плоскости для задания желаемого динамического качества проектируемой системы управления?
2. Технологические требования к проектируемой системе управления не допускают перерегулирования входного сигнала y(t) более 1% при ступенчатом входном воздействии u(t). Какое стандартное распределение полюсов следует выбрать в качестве критерия качества управления?
3. Какой из рассмотренных здесь фильтров имеет амплитудно-частотную характеристику максимально приближающуюся к АЧХ идеального фильтра?
№ задания |
Ответ |
1 |
n=4 |
2 |
a) распределение Бесселя; b) биномиальное распределение. |
3 |
Фильтр Баттерворта. |