Лекция № 5.

Тема: «Канонические формы уравнений состояния»

Математические модели объектов управления первоначально получаются на основе расчетных данных и физического поведения объекта. В этом случае переменные состояния представляют собой физические переменные объекта, и описания в пространстве состояний объективно связываются с физической реальностью.

В некоторых случаях, однако, полезно ввести переменные состояния, которые формально определяются как линейная комбинация различных физических переменных. Такое преобразование выполняется в целях получения определенных канонических форм уравнений состояния, что облегчает обнаружение некоторых свойств объекта и системы или позволяет описать их с помощью меньшего числа параметров, а также установить для односвязных систем (с одним входом и одним выходом) непосредственную связь векторно-матричных моделей с моделями типа “вход - выход”.

Рассмотрим n-мерный вектор - допустимый вектор состояния некоторой системы и невырожденную матрицу T (n x n). Тогда вектор z=Tx - также возможный вектор состояния рассматриваемой системы.

Реальная система с вектором состояния x описывается следующими уравнениями при D=0:

(5.1)

Эта же система с вектором состояния z:

(5.2)

Подставляя выражение x=T^{- 1} z в (5.1) , получим

(5.3)

Умножая первое уравнение (5.3) слева на T, получим

(5.4)

Сравнивая (5.4) и (5.2), легко установим, что

(5.5)

Таким образом, матрицы А, В, С зависят от используемого координатного базиса.

Интерес представляют инварианты, полученные после преобразования.

Теорема 5.6. Характеристическое уравнение непрерывной и дискретной систем является инвариантом, если новые состояния вводятся через невырожденную матрицу Т.

Для доказательства теоремы запишем характеристический полином матрицы ^zA:

(5.6)

Таким образом, характеристическое уравнение матрицы состояния и ее собственное значение не зависят от базиса пространства состояний.

Следовательно, можно утверждать, что свойства систем не изменяются при изменении базиса пространства состояний.

Например, ранг матрицы управляемости не изменяется, так как

(5.7)

или в краткой форме

(5.8)

Ранг матрицы наблюдаемости также не изменится, поскольку

(5.9)

или

(5.10)

Из (5.8) и (5.10) могут быть получены полезные соотношения для поиска соответствующей матрицы преобразования:

(5.11)

Особый интерес представляют так называемые канонические формы, названные в силу их простоты и непосредственной связи элементов матрицы состояния с коэффициентами характеристического уравнения или для односвязных систем с коэффициентами полиномов передаточной функции.

Каноническая форма управляемости

Здесь и далее остановимся на рассмотрении только односвязных динамических систем.

Предположим, что характеристическое уравнение матрицы А имеет вид

(5.12)

и матрица управляемости не вырождена. Тогда существует такое преобразование, при котором преобразованная система имеет вид

(5.13)

или в компактной форме

(5.14)

Соответствующая передаточная функция системы, описываемой уравнениями состояния (5.13), имеет вид

(5.15)

Матрица преобразования ВММ в каноническую форму управляемости может быть найдена по уравнениям (5.11). Однако этот процесс трудоемкий, поэтому можно использовать другие существующие способы ее определения.

Первый способ основан на использовании так называемой матрицы Фробениуса [14], которая представляет собой матрицу состояния системы в не рассматриваемой здесь канонической форме достижимости, или

(5.16)

где

(5.17)

- матрица управляемости размером n x n, а₀, а₁,..., а_n-1 - коэффициенты характеристического уравнения (5.12), которые могут быть найдены в результате расчета матрицы Фробениуса.

Матрица преобразования ^vT вычисляется с помощью следующего выражения

(5.18)

Таким образом, алгоритм преобразования ВММ к канонической форме управляемости (5.14) включает в себя следующие операции:

1. Вычисление матрицы управляемости Q_у согласно (5.17).

2. Вычисление матрицы Фробениуса F по формуле (5.16), транспонирование F для определения ^vA=F^T.

3. Вычисление матрицы ^vQ линейного преобразования по формуле (5.18).

4. Вычисление матрицы выхода, определяющей выходную переменную y по новому вектору состояния z:

(5.19)

Второй способ позволяет вычислить матрицу преобразования ^vQ рекуррентно по столбцам q_i

Действительно, на основании приведенных выше рассуждений можно записать:

или

Так как вектор ^vB известен, то мы можем сначала вычислить

и далее продолжить вычисления по отдельным столбцам справа налево:

(5.20)

Последняя строка может служить для контроля.

Коэффициенты a_i, i=0,1,2,...,n-1, матрицы ^vА можно определить с помощью определителя .

Пример 5.1. Выполним переход к канонической форме управляемости для непрерывной ВММ электродвигателя постоянного тока.

В пространстве состояния получим

(5.21)

Запишем характеристическое уравнение системы

из которого следует, что матрицы состояния и управления в новом координатном базисе будут иметь следующий вид

Определим матрицу преобразования Q.

Первый способ. Используем выражение (5.18) , которое для нашего примера запишется следующим образом

Такой же результат получается и по второму способу. Из выражения (5.20) получаем

Теперь определим матрицу ^vC в новом координатном базисе

Таким образом, ВММ нашего объекта в канонической форме управляемости принимает следующий вид

Каноническая форма наблюдаемости

Если желательно иметь матрицу в простейшей форме, то можно воспользоваться так называемой канонической формой наблюдаемости:

(5.22)

или в компактной форме

(5.23)

Как видно из выражений (5.13) и (5.22), матрицы состояний обеих канонических форм идентичны, то есть .

Для канонической формы наблюдаемости матрица наблюдаемости - единичная матрица, то есть

(5.24)

Для нахождения матрицы ^NB= ^NTB= ^NQ ^-1B матрица ^NТ может быть вычислена согласно выражению (5.11):

Так как в нашем случае , получаем, что матрица преобразования ВММ в каноническую форму наблюдаемости (5.22) соответствует матрице наблюдаемости исходной системы

(5.25)

В таком случае выражение для вычисления матрицы ^NB принимает следующий вид:

(5.26)

Пример 5.2. Выполним переход к канонической форме наблюдаемости для непрерывной ВММ электродвигателя постоянного тока (5.21).

Здесь нам необходимо только определить новое содержание матрицы ^NB. Для этого воспользуемся выражением (5.26)

Таким образом, ВММ нашего объекта в канонической форме наблюдаемости принимает следующий вид

Основные свойства объектов и систем управления можно оценить в автоматизированном режиме с помощью подсистемы Анализ Компьютерного комплекса функционального проектирования динамических систем (FuncPro 1.0). На рис. 5.1 приведено основное окно подсистемы, в котором раскрыто меню «Анализ»

1. Какие свойства и характеристики системы изменятся после преобразования ее векторно-матричной модели к новому координатному базису с помощью невырожденной матрицы Т.

2. Допустим, что нам необходимо привести ВММ непрерывной системы с одним входом и одним выходом

к канонической форме управляемости. Предварительно определены коэффициенты характеристического уравнения системы и матрица преобразования . Для вычисления какой матрицы преобразованной системы будет использована матрица Q.

3. Допустим, что нам необходимо привести ВММ непрерывной системы с одним входом и одним выходом

к канонической форме наблюдаемости. Предварительно определены коэффициенты характеристического уравнения системы и матрица преобразования . Для вычисления какой матрицы преобразованной системы будет использована матрица Q.

4. Какова будет матрица наблюдаемости непрерывной системы

№ задания	Ответ
1	внутреннее содержание матриц состояния А(Ф), управления по состоянию В(Г), выхода С.
2	матрицы выхода по состоянию
3	матрицы управления ;
4
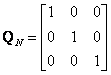