Лекция № 3.

Тема: «Вычислительные алгоритмы формирования векторно-матричных моделей в дискретном времени»

Рассмотренные примеры формирования векторно-матричных моделей показывают, что указанная процедура является трудоемкой и практически не может быть выполнена для реальных объектов. Поэтому представляют определенный интерес вычислительные алгоритмы построения дискретных моделей. Рассмотрим некоторые из них.

Алгоритм 1. Вычисление матричной экспоненты с помощью степенного ряда при заданном значении периода квантования Т.

Получение относительно точного решения с помощью приведенного в предыдущей лекции степенного ряда

(3.1)

сопряжено с необходимостью вычисления высоких степеней матрицы А. Однако с помощью алгоритма, построенного на основании теоремы Кели-Гамильтона матричная экспонента может быть вычислена с помощью (n-1) степеней матрицы А.

Согласно этому алгоритму вычисление матриц Ф и Г производится в несколько этапов (шагов).

Шаг 1: вычисляют первые (n - 1) степеней матрицы A.

Шаг 2: вычисляют коэффициенты характеристического уравнения

(3.2)

по следующим формулам:

(3.3)

где T_k=t_r(A^k) - след матрицы A^k.

Шаг 3: согласно теореме Кели-Гамильтона n - ая степень матрицы вычисляется через коэффициенты характеристического уравнения как

(3.4)

a (n + m)-я степень матрицы A находится с помощью последовательного умножения этого соотношения на матрицу A.

(3.5)

для m=0,1,2...; где

(3.6)

а остальные коэффициенты определяются из рекуррентных соотношений:

(3.7)

Шаг 4: для любого заданного T функцию e^AT можно записать как

(3.8)

Таким образом, функцию e^AT можно определить с любой заданной точностью с помощью уже вычисленных матриц A², A³,..., A ^n-1 и коэффициентов q_ij без вычисления и суммирования степеней матрицы A выше (n-1).

Интегрирование матричной экспоненты при разложении в ряд заменяется взвешенной суммой

(3.9)

которая вычисляется аналогично матричной экспоненте

(3.10)

Применение соотношений (3.8-3.10) возможно только в том случае, если заранее определена величина периода квантования.

К преимуществам данного метода можно отнести простоту алгоритма построения, быструю сходимость и малое время расчета при малых значениях Т. А то обстоятельство, что алгоритм не требует вычисления высоких степеней матрицы, позволяет избежать зацикливания исполняющей программы, если заданная точность не достигается в результате плохой сходимости степенного ряда. Однако алгоритм усложняется этапами вычисления коэффициентов характеристического уравнения и рекуррентных соотношений, требующих введения в вычислительный процесс дополнительных переменных.

Методы вычисления матричной экспоненты разложением в степенной ряд имеют существенный недостаток - изменение периода квантования требует повторения всех этапов алгоритма.

Кроме того, сходимость алгоритма и точность решения для конкретной модели определятся значением периода квантования Т. Определение критического значения Т_max является проблемой, аналогичной проблеме выбора шага численного решения дифференциальных уравнений с использованием одношаговых методов. Это обстоятельство существенно ограничивает использование данного алгоритма конструирования ВММ в дискретном времени.

Алгоритм 2. Вычисление матричной экспоненты при неизвестном значении периода квантования Т.

Особую актуальность представляют символьно-численные алгоритмы формирования дискретной ВММ, когда величина периода квантования заранее неизвестна.

Для этих целей могут быть использованы представление e^AT в виде функции от матрицы. Анализ известного математического аппарата вычисления функций от матриц показывает, что наиболее приемлемым методом вычисления матричной экспоненты является формула Сильвестра [12], согласно которой

(3.11)

где - различные собственные значения матрицы A (то есть ), m_k - кратность собственного значения как нуля минимального многочлена матрицы A, Z_kl - компоненты матрицы A, определяемые через значения приведенной присоединенной матрицы.

Если характеристический многочлен матрицы А 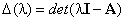имеет все различные нули, то m_k=1 для k=1,2, … ,n и минимальный многочлен совпадает с характеристическим. При этом основная формула теоремы Сильвестра приводится к следующему виду:

(3.12)

Если первоначально считать период квантования неизвестным, то будет целесообразным представить матрицы Ф и Г формируемой ВММ трехмерными Ф(n x n x n), Г(n x m x n).

В этом случае матрицы дискретной модели записывается как произведение некоторых матричных коэффициентов, умноженных на собственные моды , то есть

(3.13)

Таким образом, трехмерные матрицы дискретных моделей содержат n квадратных коэффициентных матриц F_i или G_i и при выбранном значении периода квантования Т численное значение каждого элемента матриц вычисляется по формулам

(3.13)

Причем моды комплексных собственных значений записываются через синус и косинус, например, для значения корней характеристического полинома определяются численным методом по алгоритму, в основу которого положен метод нахождения комплексных корней многочлена Берстоу [12].

Рациональность такого способа формирования дискретных ВММ объясняется, прежде всего, тем, что наиболее трудоемкие вычислительные операции по определению постоянных матричных коэффициентов выполняются один раз для любого количества исследуемых значений периода квантования. Такого никак нельзя добиться при использовании степенного ряда.

Для подтверждения преимуществ символьно-численного алгоритма рассмотрим варианты формирования дискретной модели непрерывного объекта 3-го порядка, представляющего собой линеаризованную модель сериесного электродвигателя.

В непрерывном времени объект описывается векторно-матричной моделью вида:

(3.14)

Компонентами вектора состояния здесь являются: магнитный поток - Ф, ток - i , скорость вращения ротора - .

В результате вычислительных экспериментов сформировано выражение для вычисления матричной экспоненты

Многочисленные эксперименты по оценки достоверности результатов конструирования ВММ в дискретном времени показывают, что значения переменных состояния, вычисленные с использование построенной дискретной модели, практически не отличаются от значений координат непрерывной модели. Результаты единичного эксперимента приведены на рис. 3.1.

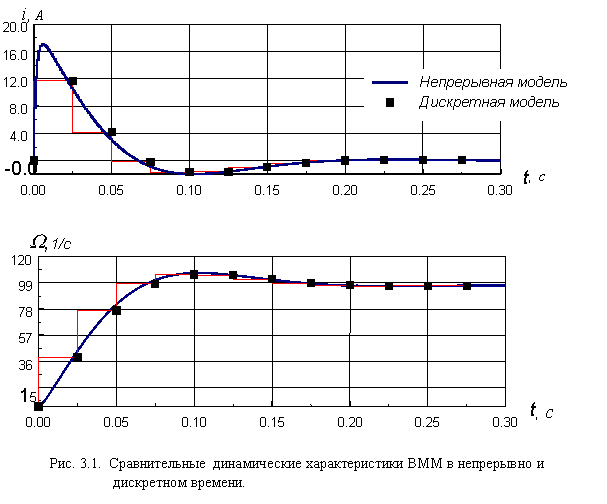
На основе вышесказанного можно сделать вывод о предпочтительном использовании символьно-численного алгоритма формирования ВММ в дискретном времени, основанного на теореме Сильвестра, что дает возможность анализировать зависимость результатов вычисления от периода квантования, а вычисленные собственные значения и коэффициенты характеристического уравнения могут быть использованы в дальнейших расчетах.

Заканчивая рассмотрение векторно-матричных моделей, целесообразно сформулировать следующие выводы.

1. Векторно-матричные модели являются высокоформализованным средством математического описания систем управления, общая структура которого не зависит от сложности объекта.

2. Проблемы автоматизации проектных процедур анализа и синтеза систем управления на основе их векторно-матричных моделей могут быть решены с помощью единого математического аппарата матричной алгебры.

3. Проектные операции построения ВММ в непрерывном времени для объектов высокого порядка, сопряженные со значительными временными затратами и определенными математическими затруднениями, должны быть автоматизированы.

4. Проектные операции построения ВММ в дискретном времени практически не осуществимы без применения ЭВМ.

1. Для построения дискретной модели непрерывного объекта 5-го порядка используется алгоритм вычисления матричной экспоненты с помощью степенного ряда 25 степени (i=0, 1, …, 25). Какую максимальную степень (k)матрицы А (A^k) при этом необходимо вычислить?

2. Укажите основной недостаток алгоритма вычисления матричной экспоненты с помощью степенного ряда.

3. Назовите главное достоинство символьно-численного алгоритма формирования дискретной векторно-матричной модели.

4. При каких условиях для вычисления матрицы состояния Ф дискретной ВММ с помощью символьно-численного алгоритма дважды используются одинаковые матричные коэффициенты, т.е. F_k= F_k+1.

ОТВЕТЫ

№ задания	Ответ
1	k=4
2	Изменение периода T квантования требует повторения всех этапов алгоритма
3	Наиболее трудоемкие вычислительные операции по определению постоянных матричных коэффициентов выполняются один раз для любого количества исследуемых значений периода квантования
4	В том случае, если имеются комплексные собственные значения матрицы А комплексно, т.е.