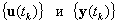Лекция № 2.

Тема: «Векторно-матричные модели систем управления в дискретном времени»

Широкое применение в теории и практике автоматического управления цифровых управляющих устройств и систем управления с ЭВМ обусловливает необходимость рассмотрения вопросов построения ВММ непрерывных объектов в дискретном времени.

Цифровые системы управления содержат как непрерывные, так и квантованные или дискретные сигналы. Наличие сигналов различного типа затрудняет описание динамического поведения системы. Однако часто можно ограничиться описанием поведения системы в моменты квантования. В этом случае сигналы выделяются только в дискретные моменты времени. Такие системы называют системами дискретного времени, они оперируют с последовательностями чисел, и, следовательно, для их описания естественно использовать разностные уравнения.

Проблема заключается в нахождении способа описания непрерывной динамической системы, связанной с ЭВМ посредством аналого-цифрового (АЦП) и цифроаналогового (ЦАП) преобразователей. Рассмотрим схему, показанную на рис. 2.1. Сигналы в ЭВМ представляют собой последовательности 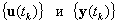, необходимо определить зависимости между ними.

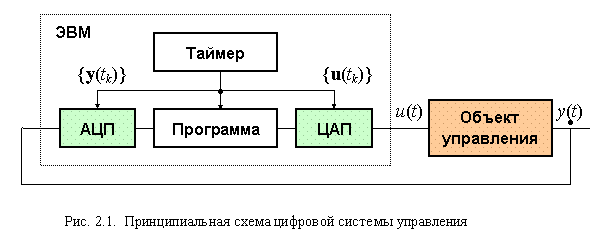
Построение дискретного эквивалента непрерывной системы называется квантованием непрерывной системы.

В дальнейшем будем считать, что непрерывная система описывается уравнениями

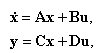
Наиболее распространенная ситуация в цифровом управлении состоит в том, что АЦП сохраняет уровень аналогового сигнала постоянным до тех пор, пока не потребуется новое преобразование

Так как управляющий сигнал прерывист, необходимо установить его поведение в точках разрыва. Допустим, что сигнал непрерывен справа и представляется дискретным процессом

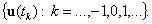(2.1)

Определим связь между переменными системы в моменты квантования. При заданном состоянии в момент квантования t_k состояние в некоторый момент t можно получить, решив систему (2.1).

Первому уравнению системы (2.1) соответствует однородное уравнение

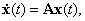(2.2)

решение которого равно

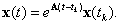(2.3)

Обозначим 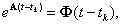тогда решение уравнения можно представить как

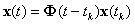(2.3)

Допустим, что решение неоднородного уравнения имеет вид

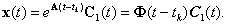(2.4)

Дифференцируя (2.4) по t, получим

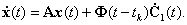(2.5)

Сравнение первого уравнения системы (2.1) и уравнения (2.5) позволяет получить следующее соотношение:

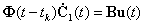(2.6)

откуда

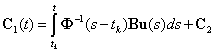(2.7)

Подставим (2.7) в (2.4), тогда

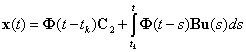(2.8)

Здесь учтено, что

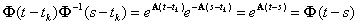
Вектор С₂ определяется по начальным условиям. При t=t_k

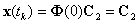
Таким образом,

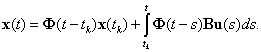(2.9)

На основании решения (2.22) определим состояние и выход системы в следующий момент квантования t_k+1 :

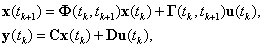(2.10)

где

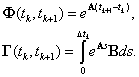(2.11)

Заметим, что характеристики системы между моментами ее квантования дают представление о реакции системы на ступенчатые воздействия с начальными условиями. Это означает, что между моментами квантования система функционирует как разомкнутая.

Для периодического квантования с периодом Т, t_k=kT, модель (2.10) сводится к стационарной системе, которую будем рассматривать в дальнейшем. Для простоты записи примем Т=1, тогда

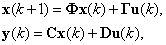(2.12)

где

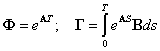(2.13)

Если матрица А не особая, то возможна запись

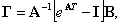(2.14)

где I- единичная матрица.

Таким образом, для получения ВММ непрерывной системы в дискретном времени требуется вычислить матричную экспоненту и проинтегрировать ее.

Вначале рассмотрим простейший случай. Используя разложение матричной экспоненты в ряд, получим следующие выражения:

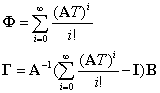(2.15)

При i=1 выражения (2.15) принимают вид

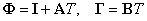(2.16)

По существу такая аппроксимация совпадает с простейшим методом решения дифференциальных уравнений по Эйлеру.

Модель (2.16) будем называть дискретной моделью по Эйлеру.

Более точное нахождение матриц Ф и Г может быть осуществлено различными способами, в том числе такими, как:

• разложение матричной экспоненты в ряд;
• применение преобразования Лапласа

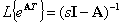(2.17)

• использование теоремы Гамильтона - Кэли.

Применение указанных способов проиллюстрируем примерами.

Разложение матричной экспоненты в ряд

Пример 2.1. Получим ВММ в дискретном времени для интегратора второго порядка, структурная схема которого приведена на рис. 2.2. Динамический процесс для такого объекта при 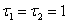описывается дифференциальным уравнением

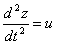(2.18)

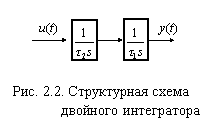
Вводя 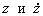как состояния системы, получим векторно-матричную запись уравнения (2.18)

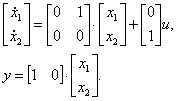(2.19)

Определим матрицы Ф и Г разложением матричной экспоненты в ряд.

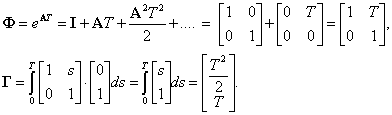(2.20)

Так как А²=0, приведенный ряд сходится точно.

Таким образом, векторно-матричная модель двойного интегратора в дискретном времени имеет вид

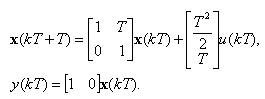(2.21)

Использование преобразования Лапласа.

Пример 2.2. Для непрерывной модели электродвигателя постоянного тока будем считать, что L_я=0, M_с=0. Тогда уравнения электродвигателя будут иметь вид

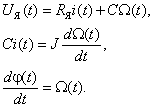или

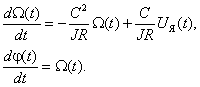В нормализованной форме записи значений параметров электродвигателя, то есть при 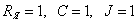в пространстве состояния 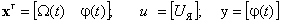получим следующую запись ВММ в непрерывном времени.

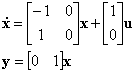
Найдем изображение матричной экспоненты по Лапласу:

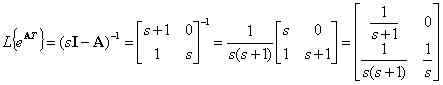
Вычисляя обратное преобразование элементов полученной матрицы, получим матрицу

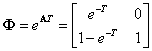
Для нахождения матрицы Г используем выражение (2.32):

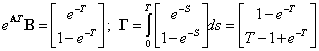
Таким образом, векторно-матричная модель рассматриваемой системы в дискретном времени имеет вид

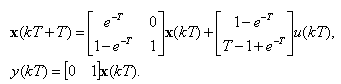(2.22)

Использование теоремы Гамильтона - Кэли.

Для систем с реальными параметрами чаще всего применяют теорему Гамильтона - Кэли, согласно которой любую функцию квадратной матрицы

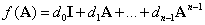
можно вычислить через характеристический полином

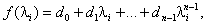
где 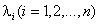- корни характеристического уравнения матрицы А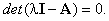

Пример 2.3. Применяя указанную теорему, построим ВММ в дискретном времени для непрерывной системы

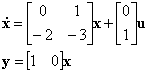
Первоначально определим корни характеристического уравнения

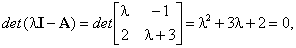
решение которого дает следующие значения:.

Так как порядок матрицы равен 2, имеем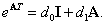

Коэффициенты 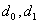определяем из системы уравнений

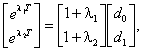
решение которой имеет вид

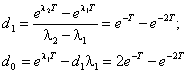
Следовательно,

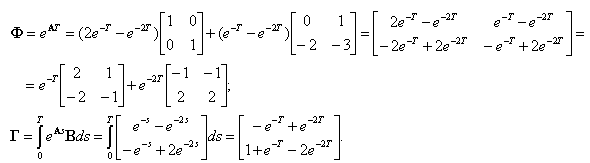(2.23)

1. Запишите дискретную модель по Эйлеру для непрерывного объекта представленного следующей векторно-матричной моделью в непрерывном времени

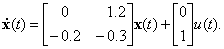
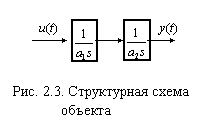
2. Для непрерывного объекта, представленного на рис. 2.3 в виде структурной схемы, определите внутреннее содержание матриц Ф, Г, С векторно-матричной модели в дискретном времени с периодом квантования Т.

3. Непрерывный объект в дискретном времени с периодом квантования Т представлен векторно-матричной моделью следующего вида

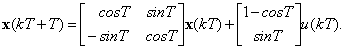
Запишите уравнение состояния этого объекта в непрерывном времении.

№ задания	Ответ
1
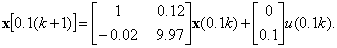2
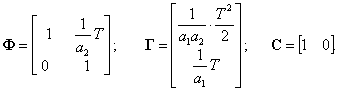3
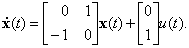