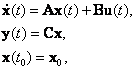
(12.1)
Тема: «Наблюдатель состояния пониженного порядка»
Для получения рациональной оценки координат вектора состояния при отсутствии шумов в измерениях Люенбергером был предложен метод, позволяющий восстанавливать только требуемые переменные вектора состояния системы.
Рассмотрим линейную наблюдаемую стационарную систему
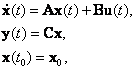 |
(12.1) |
в которой y(t) - m- мерный вектор выходных координат, причем m < n и rang C=m, т.е. имеется m линейно независимых уравнений для определения m переменных вектора состояния по вектору выхода y(t). Следовательно, порядок наблюдателя может быть снижен до (n - m).
Предположим, что оценка вектора состояния системы может быть выполнена с помощью фильтра (n - m)-го порядка
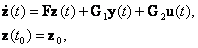 |
(12.2) |
где z(t) - (n - m)- мерный вектор состояния; F, G1, G2 - матрицы с размерами (n - m)x(n - m), (n - m)x m , (n - m)x z соответственно.
Определим условия, которым должны удовлетворять матрицы F, G1, G2 фильтра (12.2). Допустим, что параметры фильтра можно подобрать такие, чтобы
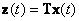 |
(12.3) |
Умножим обе части уравнения (12.2) слева на матрицу Т, тогда с учетом (12.1) получим
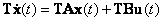 |
(12.4) |
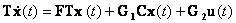 |
(12.5) |
Из равенств (12.4), (12.5) следует
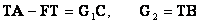 |
(12.6) |
Оценку вектора состояния будем искать в виде
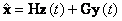 |
(12.7) |
где Н и G -матрицы с размерами n x(n - m) и (n x m) соответственно.
Потребуем выполнение условия 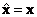 , т.е.
, т.е.
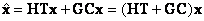 |
(12.8) |
откуда следует, что
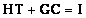 |
(12.9) |
где I - единичная матрица.
Элементы пяти матриц: F, G1, G2, G, H, связанные уравнениями (12.6), (12.9), могут выбираться до некоторой степени произвольно.
Векторно-матричная модель системы управления с наблюдателем Люенбергера при 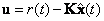 имеет следующий вид:
имеет следующий вид:
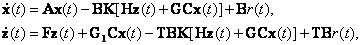 |
(12.10) |
или
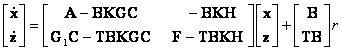 |
(12.11) |
Наблюдатель Люенбергера не изменяет полюсы замкнутой системы управления, а лишь добавляет к ним свои собственные.
Таким образом, синтез наблюдателя пониженного порядка может выполняться по следующему алгоритму.
1. Проверить наблюдаемость исходной системы с определением индекса наблюдаемости m.
2. Выполнить анализ матрицы состояния А объекта управления с определением корней характеристического уравнения.
3. Выбрать матрицу F таким образом, чтобы обеспечить требуемое время переходного процесса в наблюдателе.
4. Произвольно задать матрицу G1, соблюдая при этом выполнение условия управляемости фильтра (12.2) по вектору y(t), т.е. необходимо, чтобы
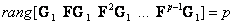 |
|
где p=n - m .
5. Решить матричное уравнение 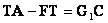 относительно Т.
относительно Т.
6. Вычислить матрицу 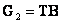 .
.
7. Вычислить матрицы Н и G из уравнения (12.9).
Общая схема системы управления с наблюдателем пониженного порядка будет иметь вид, представленный в среде компьютерного комплекса FuncPro 1.0 на рис 12.1.
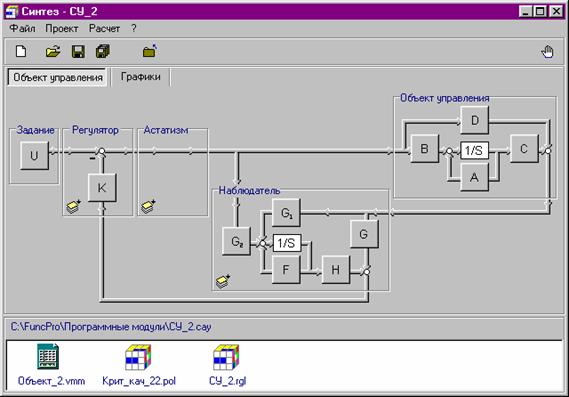
Рис. 12.1. Схема системы управления с наблюдателем пониженного порядка
Компьютерная реализация указанного алгоритма позволяет конструировать наблюдатели координат, измерение которых затруднено или практически невозможно. Так, например, для построения системы управления электромеханического объекта с упругой передачей механического движения от вала электродвигателя к валу рабочего механизма требуется измерение упругого момента. Проще и эффективнее здесь использовать вычислительное устройство, построенное как наблюдатель первого порядка, а координаты тока, скоростей электродвигателя и механизма регистрировать с помощью датчиков.
Таблица 12.1. Параметры электромеханического объекта

Выполнение отмеченной процедуры для электромеханического объекта с параметрами, приведенными в табл. 12.1., приводит следующим результатам.

Корректность полученных результатов подтверждают динамические характеристики системы с регулятором состояния и наблюдателем упругого момента, приведенные на рис. 12.2.
Регулятор состояния здесь синтезирован при использовании в качестве критерия качества биномиального распределения корней (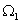 =8.5 с-1).
=8.5 с-1).
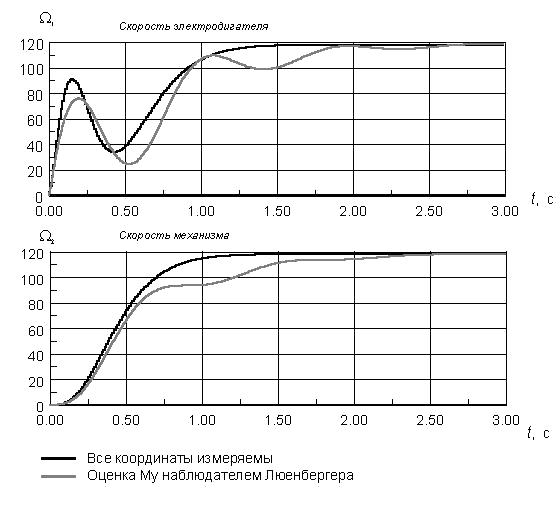
Рис. 12.2. Динамические характеристики ЭМС при непосредственном измерении всех координат и при оценке упругого момента наблюдателем пониженного порядка.
1. Какая матрица 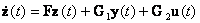 определяет требуемое время оценки неизмеряемых компонент вектора состояния системы с помощью наблюдателя Люенбергера?
определяет требуемое время оценки неизмеряемых компонент вектора состояния системы с помощью наблюдателя Люенбергера?
2. Из каких условий выбирается матрица G1 фильтра 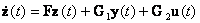 необходимого для синтеза наблюдателя Люенбергера?
необходимого для синтеза наблюдателя Люенбергера?
№ задания |
Ответ |
1 |
Матрицы F |
2 |
Матрицу G1 можно задавать произвольно, соблюдая при этом условия управляе-мости фильтра (12.2) по вектору y(t), т.е. необходимо, чтобы 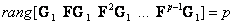 где p=n - m |