Лекция № 11.

Тема: «Оценка вектора состояния при случайных возмущениях и наличии помех»

При решении практических задач очень часто возникает ситуация, когда необходимые для управления координаты вектора состояния объекта не измеряются или измеряются с существенными случайными ошибками, а движение объекта управления подвержено случайным воздействиям. В таких ситуациях управление определяется на основе результатов оценивания состояния системы, которое имеет статистическую связь с данными наблюдений.

Рассмотрим алгоритм линейной оценки вектора состояния системы с минимальной дисперсией.

Пусть динамическая система описывается векторным дифференциальным уравнением.

(11.1)

Здесь, кроме представленных ранее матриц и векторов, w(t)- k-мерный вектор случайных воздействий; Т- матрица размером n x k.

Вектор измеряемых выходных координат, который доступен наблюдению, определяется соотношением

(11.2)

где v(t) - m-мерный вектор случайных помех, сопровождающих измерения.

Предполагается, что система (11.1), (11.2) при w(t) 0 и v(t) 0 наблюдаема. Будем считать w(t) и v(t) гауссовскими случайными процессами типа белого шума с нулевыми математическими ожиданиями

и корреляционными матрицами

(11.3)

где - дельта-функция; Q(t)- симметричная неотрицательно определенная k x k - матрица интенсивности белого шума w(t);

R(t)- симметричная положительно определенная m x m - матрица интенсивности белого шума v(t).

Допустим, что начальное состояние системы х(t0)- n-мерный случайный вектор с известным математическим ожиданием

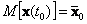
и корреляционной матрицей

(11.4)

Кроме того, будем считать, что х(t0), w(t), v(t) взаимно не коррелированны.

Найти необходимо линейную несмещенную оценку вектора х(t0), построенную на основе наблюдения , .

Несмещенная оценка предполагает равенство ее математического ожидания математическому ожиданию истинной величины .

(11.5)

Предположим, что получается на выходе фильтра

(11.6)

Чтобы процесс на выходе фильтра был несмещенной оценкой, должно выполняться равенство (11.5). Вычислим математическое ожидание обеих частей уравнения (11.6):

(11.7)

но из (11.2) следует, что

(11.8)

На основании (11.6) - (11.8) получим дифференциальное уравнение для среднего значения вектора состояния системы:

(11.9)

Вычисляя математическое ожидание от (11.13), получим еще одно уравнение для среднего значения вектора состояния

(11.10)

Сравнивая (11.10) и (11.9), определим первое условие несмещенности оценки вектора состояния:

(11.11)

Второе условие состоит в том, чтобы уравнения (11.21) и (11.22) решались при одном и том же начальном условии

(11.12)

При выполнении этих условий уравнение фильтра примет вид

(11.13)

Остается определить матрицу коэффициентов усиления фильтра L(t), которая обеспечила бы оптимальную оценку в том смысле, что составляющие ошибки оценивания должны иметь минимальную дисперсию.

Согласно принципу дуальности и с учетом того, что дисперсия случайной функции представляет собой среднее значение квадрата разности между случайной функцией и ее средним значением, можно утверждать, что матрица коэффициентов усиления оптимального фильтра определяется выражением

(11.14)

которое получается по алгоритму синтеза оптимального управления для сопряженной системы

Здесь P(t) - корреляционная матрица ошибок оценивания, является решением матричного дифференциального уравнения Риккати

(11.27)

Наблюдатель, построенный по приведенному алгоритму, называют оптимальным фильтром Калмана – Бьюси.

Для стационарной системы, в которой A, B, C, T, Q, R- коэффициентные матрицы, уравнение фильтра Калмана - Бьюси принимает вид

(11.28)

Матрица коэффициентов усиления фильтра постоянна и определяется выражением

(11.29)

где Р- положительно определенная матрица, являющаяся решением алгебраического матричного уравнения Риккати

(11.30)

Многочисленные вычислительные эксперименты, выполненные в целях анализа систем управления с наблюдателями, построенными по принципу фильтра Калмана - Бьюси при учете помех и случайных возмущений, подтверждают корректность приведенных алгоритмов и компьютерных средств их реализации. На рис. 11.1 приведены сравнительные динамические характеристики упругого электромеханического объекта, системы управления которого построены как при непосредственном изменении координат, так и при использовании наблюдателя (11.25). При постановке экспериментов с моделью ЭМС с наблюдателем случайные возмущения и помехи имитированы с помощью гармонических сигналов, а регуляторы и наблюдатели представлены в дискретном виде с помощью разностных уравнений.

1. Какой из рассмотренных ранее алгоритмов используется для вычисления матрицы коэффициентов усиления оптимального фильтра?

2. При каких условиях матрица коэффициентов усиления фильтра Калмана-Бьюси постоянна во времени?