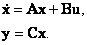
(10.1)
Тема: «Наблюдатель состояния полного порядка»
При решении практических задач управления методами теории пространства состоя-ний мы часто встречаемся со случаями, когда часть переменных вектора состояния оказыва-ются неизмеримыми. Если имеется математическая модель системы, то можно попытаться вычислить состояние системы по наблюдаемым входам и выходам.
Восстановление вектора состояния x(t) называется его оценкой, а устройство, обеспе-чивающее получение оценки по измерениям управления u (t) и вектора выхода y(t) на конеч-ном интервале времени, - наблюдателем.
Пусть стационарный объект описывается традиционной системой уравнений
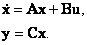 |
(10.1) |
Предположим, что матрицы A, B, C известны, тогда вектор x можно аппроксимиро-вать состоянием 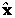 модели
модели
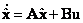 |
(10.2) |
которая имеет тот же вход, что и объект (10.1).
Если модель (10.2) является идеальной аппроксимацией системы (10.1), в том смысле, что их параметры и начальные условия идентичны, то состояния x и 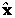 также совпадают. Если начальные условия для систем (10.1) и (10.2) различны, то
также совпадают. Если начальные условия для систем (10.1) и (10.2) различны, то 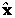 сходится к x только то-гда, когда система (10.1) асимптотически устойчива.
сходится к x только то-гда, когда система (10.1) асимптотически устойчива.
При восстановлении (10.2) не используется измеряемый выход. Качество восстанов-ления улучшается, если ввести в модель разность измеренного выхода и его оценки 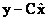 в виде обратной связи:
в виде обратной связи:
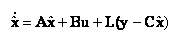 |
(10.3) |
Здесь L - некоторая матрица, обеспечивающая требуемый вид переходных процессов оценки вектора состояния.
Введем ошибку восстановления
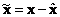 |
(10.4) |
Вычитая (10.3) из дифференциального уравнения (10.1), получим
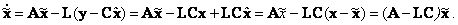 |
(10.5) |
Очевидно, для того чтобы ошибка восстановления стремилась к нулю, необходимо выбрать матрицу L так, чтобы система (10.5) была асимптотически устойчива.
Таким образом, вводя обратную связь в модель восстановления, можно нивелировать ошибку, даже если система (10.1) неустойчива.
Мы видим, что модель (10.3) восстанавливает все составляющие вектора состояния, поэтому она называется наблюдателем состояния полного порядка.
Общая схема системы управления с наблюдателем состояния полного порядка будет иметь вид, представленный в среде компьютерного комплекса FuncPro 1.0 на рис 10.1.
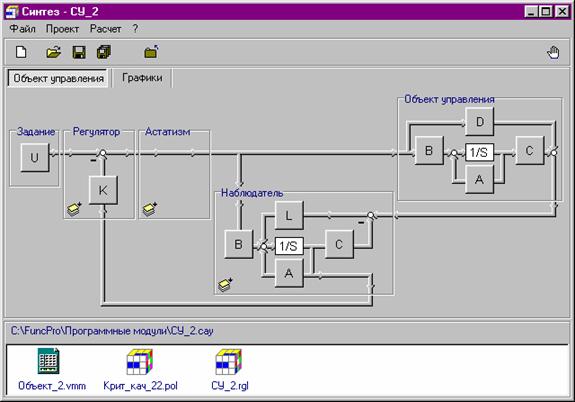
Рис. 10.1. Схема системы управления с наблюдателем полного порядка
При синтезе наблюдателей обычно используют два принципа: принцип разделимости и принцип дуальности.
Принцип разделимости. Допустим, что объект описывается уравнениями (10.1), регу-лятор состояния -
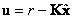 |
(10.6) |
а наблюдатель полного порядка - уравнением (10.3).
Тогда уравнения состояния всей системы имеют вид
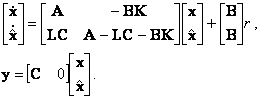 |
(10.7) |
Если ввести ошибку (10.4), то с помощью линейного преобразования
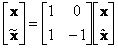
(10.8)
получим
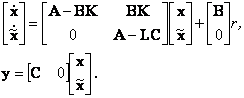 |
(10.9) |
Из (10.9) очевидно, что характеристическое уравнение всей системы имеет вид
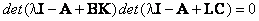 |
(10.10) |
Откуда следует, что характеристические полиномы замкнутой системы управления и наблю-дателя независимы и, следовательно, мы можем назначать полюсы наблюдателю независимо от полюсов системы управления.
Процесс, описываемый уравнениями (10.9), состоит из двух взаимно независимых процессов: из процесса оценки вектора 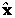 и из собственно процесса управления.
и из собственно процесса управления.
Эту возможность разделения процессов в наблюдателе и регуляторе принято называть принципом разделимости.
Принцип дуальности (приводится без доказательства). Условием наблюдаемости сис-темы (10.1) одновременно является полная управляемость сопряженной системы
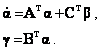 |
(10.11) |
С учетом принципов дуальности и разделимости синтез наблюдателя состояния вы-полняется независимо от синтеза регулятора состояния по алгоритмам, изложенным в 4.1.
Действительно, для системы (10.3) регулятор состояния будет иметь вид
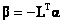 |
(10.12) |
Так как 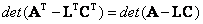 элементы матрицы L определяются по алгоритмам вычисления матрицы К для регулятора состояния.
элементы матрицы L определяются по алгоритмам вычисления матрицы К для регулятора состояния.
В этой связи, для автоматизированного выполнения проектных операций синтеза на-блюдателей состояния полного порядка могут быть использованы алгоритмы и компью-терные средства синтеза регуляторов состояния.
Многочисленные вычислительные эксперименты, выполненные в целях построения систем управления с наблюдателями полного порядка и регуляторами состояния, подтвер-ждают корректность приведенного выше положения.
На рис. 10.2 приведены сравнительные динамические характеристики упругого элек-тромеханического объекта, системы управления которого построены как при непосредствен-ном изменении координат, так и при использовании наблюдателя (10.3). Причем, при поста-новке имитационных экспериментов с моделью ЭМС с наблюдателем были изменены от-дельные параметры объекта в пределах 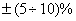 , учтены люфты в механических переда-чах и инерционность преобразователя.
, учтены люфты в механических переда-чах и инерционность преобразователя.
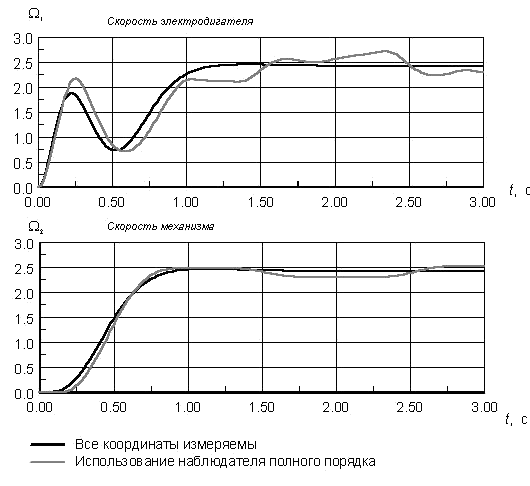
Рис. 10.2. Сравнительные динамические характеристики ЭМС при непосредственном измерении координат и использовании наблюдателя полного порядка
1. Для достижения каких целей и из каких условий выбирается матрица L наблюдателя полного порядка?
2. Назовите два основных принципа синтеза наблюдателя.
3. В какой последовательности следует выполнять проектные операции синтеза регуля-тора и наблюдателя состояния?
4. Вы решили воспользоваться методом расположения полюсов для синтеза наблюдате-ля полного порядка. С какой векторно-матричной моделью должна выполняться эта операция, если ВММ объекта управления имеет вид

№ задания |
Ответ |
1 |
Матрица L обеспечивает требуемый вид переходных процессов оценки вектора состояния и выбирается из условий достижения асимптотической устойчивости замкнутой системы объект – наблюдатель. |
2 |
Принцип разделимости и принцип дуальности. |
3 |
Проектные операции могут быть выполнены в любой последовательности. |
4 |
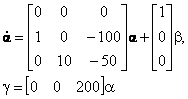 |