Под алгоритмическим базисом будем понимать совокупность средств построения моделей, методов их графического представления и алгоритмов преобразования этих моделей.
Наличие четырех уровней описания моделей, предложенных в концепции структурного моделирования динамических систем, предопределяет соответствующее разделение и алгоритмического базиса структурного моделирования.
К настоящему времени концепция структурного моделирования динамических систем может быть практически реализована с помощью отечественных и зарубежных систем моделирования при использовании в основном первых трех уровней описания структурных моделей. Среди современных разработок здесь можно отметить системы LabVIEW, Micro-Cap, VisSim, Экспресс-Радиус, МВТУ (Моделирование в технических устройствах). Наибольший интерес в указанной области представляет семейство комплексов моделирования, созданных в Ивановском энергетическом университете. При представлении материала настоящего курса будем ориентироваться на использование программно-методического комплекса МИК-АЛ [1], функционирующего под управлением MS DOS, и компьютерного комплекса IDS 1.0 [6], функционирующего под управлением Windows 9x.
Для пользователей компьютерных средств автоматизации моделирования динамических систем наибольший интерес представляют математический и функциональный уровень описания структурных моделей. Поэтому первоначально остановимся на рассмотрении этих двух уровней алгоритмического базиса.
Для специалистов в области ЭМС наиболее удобно и традиционно графическое описание моделей в виде структурных схем.
Если фрагменты математического описания разделить на блоки в соответствии с физическими процессами, протекающими в системе, определить входные и выходные координаты и внутренние параметры каждого блока и изобразить схему взаимодействия блоков, то получим структурную модель математического уровня (СММУ). Таким образом, можно утверждать, что "кирпичиками", из которых конструируется СММУ, являются динамические элементы. В общем случае динамический элемент представляется в виде блока, осуществляющего преобразования входных воздействий в выходной сигнал элементов в соответствии с заданной функцией.
Многообразие указанных функций предопределяет необходимость разделения динамических элементов на классы. Укажем наиболее используемые классы динамических элементов:
Каждый динамический элемент характеризуется следующими атрибутами:
Рассмотрим краткие характеристики элементов каждого класса.
(2.1)
Графически элемент изображается в виде прямоугольника (рис. 2.1) с одним выходом.
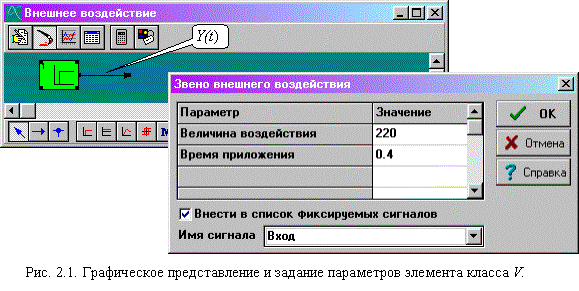
Для получения более сложных форм внешних воздействий необходимо использовать комбинации элементов возмущения с динамическими элементами других классов.
(2.2)
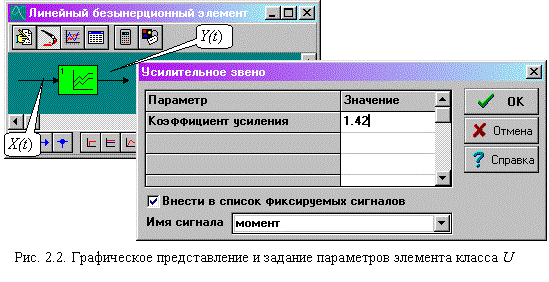
где x(t) - значение входного сигнала элемента, Ku - значение коэффициента передачи.
Графическое представление элемента класса U приведено на рис. 2.2
(2.3)
что соответствует дифференциальному уравнению n- порядка
(2.4)
при нулевых начальных условиях.
В каждый момент времени значение выходного сигнала формируется в результате численного интегрирования дифференциального уравнения (2.4)
Графическое представление элемента класса L приведено на рис. 2.3.
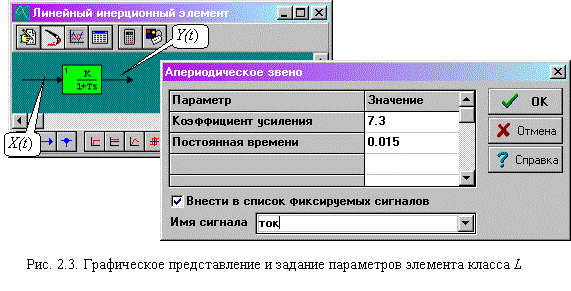
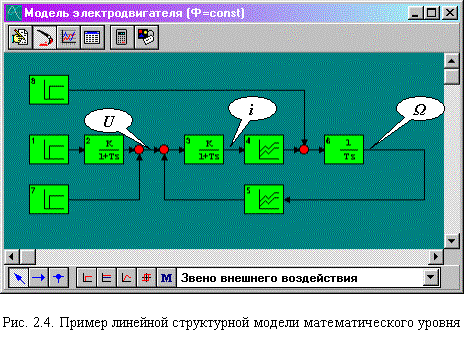
С использованием элементов перечисленных выше трех классов могут быть построены структурные модели математического уровня линейных электромеханических систем. Так, например, модель для изучения динамических процессов пуска и останова электродвигателя постоянного тока независимого возбуждения при постоянном магнитном потоке (Ф=const) принимает вид, приведенный на рис. 2.4.
Здесь электромеханические процессы преобразования энергии описаны следующей системой линейных дифференциальных уравнений:
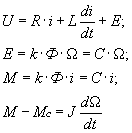
(2.5)
Входное напряжение электродвигателя U нарастает по экспоненциальному закону и мгновенно отключается при достижении модельного времени значения t=1.5
В общем случае с помощью нелинейных элементов осуществляется операция
(2.6)
где y(t) - выходной сигнал элемента, x(t) - вектор входных сигналов. A - вектор параметров,
 t - время.
t - время.
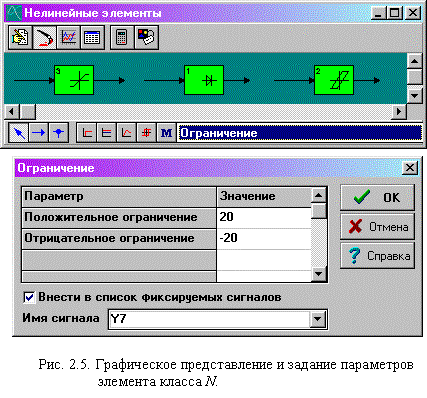
Примеры графического представления нелинейных функциональных элементов приведены на рис. 2.5.
Используя отдельные нелинейные элементы, приведенная на рис. 2.4 структурная модель может быть перестроена для изучения динамических процессов в двигателе постоянного тока при изменении магнитного потока (Ф=var) и линейном нарастании входного напряжения U до заданного уровня.(рис. 2.6).
Здесь использованы три вида нелинейных элементов:
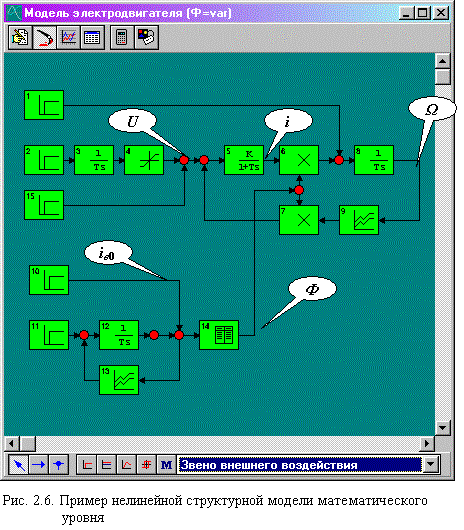
Ограничение (элемент №4) - для формирования кривой входного напряжения, Умножение (элементы 6,7) - для перемножения мгновенных значений переменных и Табличная нелинейность - для учета реальной кривой намагничивания электродвигателя
На начальном этапе изучения теоретического материала и выполнения практических заданий и лабораторного практикума, как правило, используются элементы четырех рассмотренных выше классов. Поэтому, характеристики других классов элементов мы пока приводить не будем.
Базовый состав функциональных элементов структурных моделей математического уровня приведен в приложении 1.
Структурная модель конкретной электромеханической системы конструируется из базовых элементов путем объединения точек входа и выхода и введения узлов алгебраического суммирования сигналов. Исходной информацией для построения структурных моделей математического уровня могут быть математическое описание динамических процессов в форме дифференциальных уравнений или структурная схема исследуемой системы.
С появлением средств графического взаимодействия отпала необходимость в разработке, изучении и использовании специализированных языков моделирования. К настоящему времени практически все системы моделирования имеют интерфейсные средства, позволяющие пользователю быстро и удобно нарисовать структурную модель для дальнейшей постановки имитационных экспериментов.