Лекция No 8
Особенности некоторых режимов в схемах выпрямителей
1. Коммутация в однофазных схемах
В реальных схемах из-за наличия во входной цепи переменного тока индуктивных сопротивлений, в частности индуктивных сопротивлений обмоток согласующего трансформатора или входных реакторов, процесс коммутации имеет определенную длительность, т.е. процесс перехода тока с одного вентиля на другой происходит не мгновенно, а с некоторой постоянной времени контура коммутации.

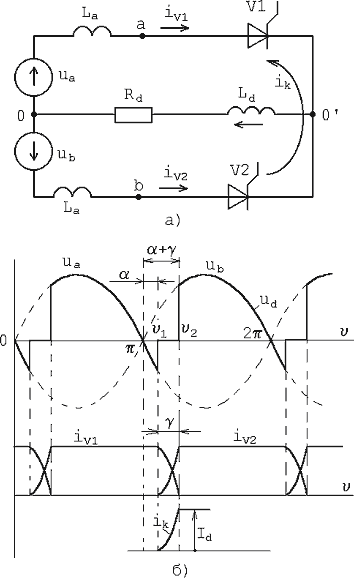
Рис.1. Процессы коммутации: а - схема; б – осциллограммы
Помимо индуктивного сопротивления, на процессы коммутации влияет и входное активное сопротивление обмоток трансформатора, но его влияние в нормальных режимах значительно меньше. Поэтому рассмотрим процессы коммутации с учетом только входных индуктивных сопротивлений (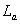 ), полагая при этом выпрямленный ток идеально сглаженным (
), полагая при этом выпрямленный ток идеально сглаженным (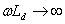 ).
).
Учитывая одинаковый характер процессов коммутации в различных вентильных схемах, остановимся на наиболее простой схеме выпрямления – однофазной двухполупериодной (рис.1,а).
Индуктивные сопротивления обмоток силового трансформатора учтены введением в схему индуктивностей 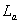 ;
; 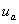 и
и 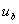 – мгновенные значения ЭДС вторичных полуобмоток.
– мгновенные значения ЭДС вторичных полуобмоток.
Предположим, что в проводящем состоянии находится вентиль 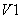 . В момент
. В момент 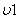 поступает отпирающий импульс на вентиль
поступает отпирающий импульс на вентиль 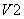 .
.
Поскольку потенциал анода вентиля 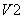 в этот момент положителен относительно катода, вентиль включается (рис.1,б).
в этот момент положителен относительно катода, вентиль включается (рис.1,б).
Начиная с момента 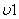 оба вентиля будут включены, и вторичные полуобмотки трансформатора оказываются замкнутыми через вентили
оба вентиля будут включены, и вторичные полуобмотки трансформатора оказываются замкнутыми через вентили 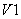 и
и 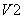 накоротко. Под воздействием ЭДС вторичных полуобмоток
накоротко. Под воздействием ЭДС вторичных полуобмоток 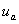 и
и 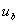 в короткозамкнутой цепи (контур коммутации) возникает ток короткого замыкания
в короткозамкнутой цепи (контур коммутации) возникает ток короткого замыкания 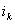 , который является коммутирующим током.
, который является коммутирующим током.
Этот ток можно в любой момент времени, начиная с 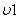 , определить как сумму двух составляющих: установившейся
, определить как сумму двух составляющих: установившейся 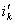 и свободной
и свободной 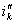 , которые рассчитываются по следующим соотношениям:
, которые рассчитываются по следующим соотношениям:
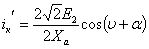 ;
;
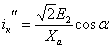 ,
,
где 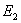 – действующее значение напряжения вторичной полуобмотки трансформатора;
– действующее значение напряжения вторичной полуобмотки трансформатора; 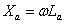 ;
; 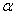 - угол управления.
- угол управления.
Результирующий ток короткого замыкания можно записать в виде
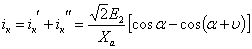 .
.
Учитывая, что выпрямленный ток при 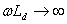 в период коммутации остается неизменным, можно записать для узла 0 или
в период коммутации остается неизменным, можно записать для узла 0 или 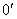 следующее уравнение токов:
следующее уравнение токов:
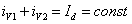 ,
,
где 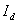 – среднее значение выпрямленного тока или тока нагрузки. Последнее уравнение справедливо для любого момента времени. Пока ток проводит только вентиль
– среднее значение выпрямленного тока или тока нагрузки. Последнее уравнение справедливо для любого момента времени. Пока ток проводит только вентиль 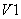 , получаем
, получаем
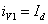 ;
; 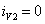 .
.
В интервале коммутационного процесса ( ) от
) от 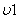 до
до 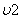 ток
ток 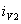 плавно увеличивается, а
плавно увеличивается, а 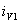 уменьшается. Когда ток
уменьшается. Когда ток 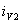 будет равным
будет равным 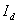 , а ток
, а ток 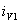 снизится до нуля, вентиль
снизится до нуля, вентиль 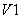 выключится, и ток нагрузки будет протекать лишь через вентиль
выключится, и ток нагрузки будет протекать лишь через вентиль 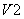 .
.
Длительность интервала коммутации характеризуется обычно углом коммутации 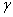 , который может быть определен для рассмотренной схемы из следующего уравнения:
, который может быть определен для рассмотренной схемы из следующего уравнения:
|
(1) |
Обозначив угол коммутации 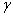 при угле
при угле 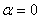 через
через 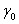 , можно записать
, можно записать
|
(2) |
подставив (2) в (1) получим
|
(3) |
Замечание 1. Длительность протекания тока в вентилях по сравнению с идеализированной схемой увеличивается на угол 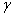 и становится равной
и становится равной 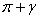 .
.
Замечание 2. Процесс коммутации оказывает непосредственное влияние на выпрямленное напряжение 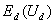 , так как на интервалах коммутации мгновенное значение выпрямленного напряжения в рассмотренной схеме снижается до нуля. В результате этого происходит уменьшение среднего значения выпрямленного напряжения на
, так как на интервалах коммутации мгновенное значение выпрямленного напряжения в рассмотренной схеме снижается до нуля. В результате этого происходит уменьшение среднего значения выпрямленного напряжения на 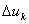 .
.
|
(4) |
Для нашего случая имеем 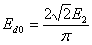 , таким образом, падение напряжения в коммутационном интервале выразится как
, таким образом, падение напряжения в коммутационном интервале выразится как
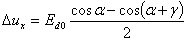
или
|
(5) |
но
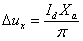 ,
,
где
|
(6) |
При непрерывных токах, т.е. токах, при которых существуют коммутационные провалы напряжения 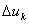 , имеем регулировочную характеристику
, имеем регулировочную характеристику 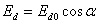 (рис.2).
(рис.2).
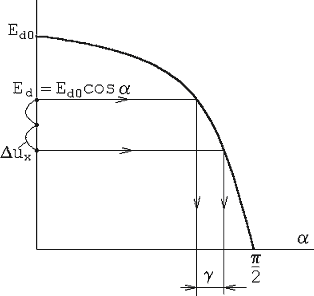
Рис.2. Регулировочные характеристики
Процедура определения угла коммутации по регулировочной характеристике (рис. 2):
находим 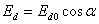 и откладываем ее на регулировочной характеристике,
и откладываем ее на регулировочной характеристике,
от точки  откладываем
откладываем 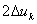 ,
,
проводим прямую, и, опустив перпендикуляры на ось 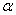 , получаем угол коммутации
, получаем угол коммутации 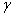 .
.
Среднее значение выпрямленного напряжения для рассмотренной схемы
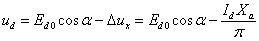 .
.
Рассмотренный принцип нахождения угла коммутации 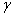 применим к любой схеме, но при условии непрерывного тока
применим к любой схеме, но при условии непрерывного тока 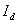 .
.
Замечание 3. Появление коммутационных участков в выпрямленном напряжении приводит к изменению его гармонического состава (5-8%). Угол коммутации влияет и на гармонический состав первичного тока (тока, забираемого из сети), потребляемого выпрямителем.
2. Влияние процесса коммутации в других схемах.
Однофазная мостовая схема по принципу действия подобна однофазной двухполупериодной схеме, рассмотренной ранее (рис.3).
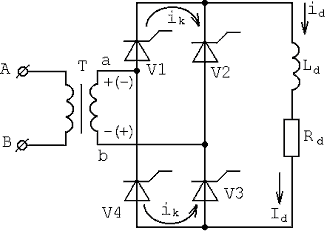
Рис.3. Мостовая однофазная схема
Отличие состоит в том, что при коммутации тока в этой схеме возникают два контура коммутации, каждый из которых состоит из двух вентилей и вторичной обмотки трансформатора: один контур – из вентилей 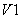 и
и 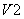 , а другой – из
, а другой – из 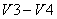 . Ток
. Ток 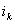 распределяется между этими контурами поровну (рис.3).
распределяется между этими контурами поровну (рис.3).
Для мостовой схемы имеем
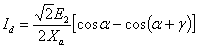 ;
; 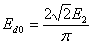 .
.
Среднее значение выпрямленного напряжения
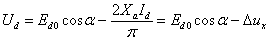 ,
,
где
|
(7) |
В многофазных схемах (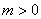 ) возникают частичные контуры короткого замыкания между отдельными фазами. При этом мгновенное значение выпрямленного напряжения не падает до нуля, а становится равным среднему арифметическому значению напряжений фаз, в вентилях которых коммутируются токи. Так, для трехфазных схем со средней точкой и мостовой мгновенное значение выпрямленного напряжения на интервале коммутации тока между вентилями фаз
) возникают частичные контуры короткого замыкания между отдельными фазами. При этом мгновенное значение выпрямленного напряжения не падает до нуля, а становится равным среднему арифметическому значению напряжений фаз, в вентилях которых коммутируются токи. Так, для трехфазных схем со средней точкой и мостовой мгновенное значение выпрямленного напряжения на интервале коммутации тока между вентилями фаз 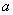 и
и 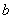 равно
равно
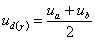 ,
,
где 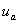 и
и 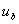 – мгновенные значения фазных напряжений вторичной обмотки трансформатора. Длительность протекания тока через вентили увеличивается на угол
– мгновенные значения фазных напряжений вторичной обмотки трансформатора. Длительность протекания тока через вентили увеличивается на угол 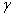 и становится равной
и становится равной 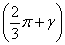 . В схемах со средней точкой и трехфазной мостовой угол коммутации
. В схемах со средней точкой и трехфазной мостовой угол коммутации 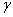 связан с выпрямленным током
связан с выпрямленным током 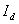 и углом
и углом 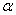 следующим соотношением:
следующим соотношением:
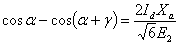 .
.
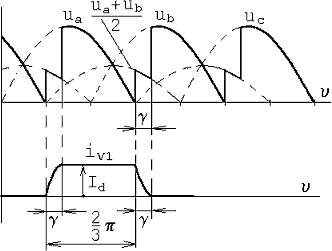
Рис.4. Процесс коммутации в трехфазной схеме
Падение напряжения 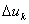 , на которое уменьшаются средние значения выпрямленного напряжения, равно:
, на которое уменьшаются средние значения выпрямленного напряжения, равно:
в трехфазной схеме со средней точкой
|
(8) |
в трехфазной мостовой схеме
|
(9) |
Часто встречается выражение 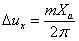 , что не всегда оправдано, т.к. есть еще коэффициент схемы.
, что не всегда оправдано, т.к. есть еще коэффициент схемы.
3. Внешние характеристики выпрямителей
Внешней характеристикой выпрямителя называется зависимость выпрямленного напряжения от среднего значения тока нагрузки, т.е. 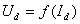 .
.
Внешняя характеристика определяется внутренним сопротивлением выпрямителя, которое приводит к снижению выпрямленного напряжения с ростом нагрузки. Снижение напряжения обусловлено активным сопротивлением схемы выпрямителя 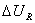 , падением напряжения в вентилях
, падением напряжения в вентилях 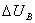 и индуктивным сопротивлением
и индуктивным сопротивлением 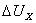 , которое проявляется при процессах коммутации.
, которое проявляется при процессах коммутации.
Соответственно внешнюю характеристику выпрямителя (при 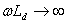 ) можно записать в виде следующего уравнения:
) можно записать в виде следующего уравнения:
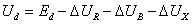 ,
,
где 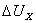 находится по выражениям (7-9);
находится по выражениям (7-9);
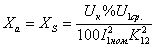 ;
; 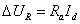 ;
; 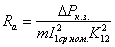 ;
; 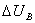 – падение напряжения на вентилях (0.5...2)В.
– падение напряжения на вентилях (0.5...2)В. 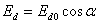 - в режиме непрерывных токов;
- в режиме непрерывных токов; 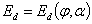 - из регулировочной характеристики для каждого частного случая;
- из регулировочной характеристики для каждого частного случая; 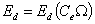 - при работе выпрямителя на якорь двигателя постоянного тока [1].
- при работе выпрямителя на якорь двигателя постоянного тока [1].
4. Работа выпрямителей на противо-ЭДС
Рассмотрим влияние противо-ЭДС на электромагнитные процессы в схеме выпрямителя на примере однофазной схмы со средней точкой, в цепь постоянного тока которой включена аккумуляторная батарея с ЭДС Е0 и внутренним сопротивлением Rd (рис.5,а).
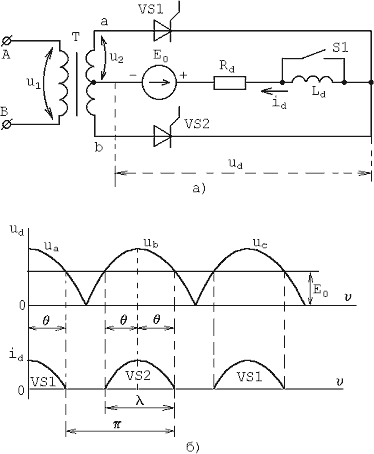
Рис.5. Выпрямитель с противо-ЭДС: а – схема, б – диаграммы напряжения и тока
Предположим, что ключ 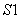 замкнут, т.е. индуктивность
замкнут, т.е. индуктивность 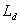 отсутствует. В этом случае ток
отсутствует. В этом случае ток 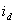 в нагрузке начинает протекать, когда мгновенное значение выпрямленного напряжения
в нагрузке начинает протекать, когда мгновенное значение выпрямленного напряжения 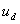 превышает ЭДС
превышает ЭДС 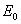 (рис.5,б), так как только при этом условии к вентилям схемы будет приложено прямое напряжение, и они будут проводить ток.
(рис.5,б), так как только при этом условии к вентилям схемы будет приложено прямое напряжение, и они будут проводить ток.
Ток id, протекающий в этом случае в цепи нагрузки, можно выразить следующей формулой, приняв за начало отсчета максимум выпрямленного напряжения:
|
(10) |
Очевидно, что интервал проводимости вентилей будет зависеть от соотношения амплитуды напряжения вторичной обмотки трансформатора 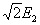 и противо-ЭДС
и противо-ЭДС 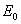 . Тогда интервал проводимости вентилей
. Тогда интервал проводимости вентилей 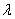 можно записать в виде
можно записать в виде
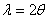 .
.
Учитывая, что отсчет ведется от максимума выпрямленного напряжения, можно записать
|
(11) |
или
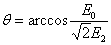 .
.
Подставляя (11) в (10), получаем следующее выражение для мгновенного значения тока в нагрузке:
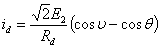 .
.
Среднее значение выпрямленного тока (постоянную составляющую) можно определить из соотношения
|
(12) |
Для схемы 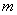 -фазного выпрямителя уравнение (12) принимает вид
-фазного выпрямителя уравнение (12) принимает вид
|
(13) |
где 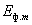 – амплитуда фазного напряжения вторичной обмотки трансформатора.
– амплитуда фазного напряжения вторичной обмотки трансформатора.
Если в цепь постоянного тока включена индуктивность 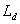 (ключ
(ключ 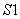 разомкнут), то пульсация выпрямленного тока уменьшается и при
разомкнут), то пульсация выпрямленного тока уменьшается и при 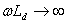 становится равной нулю. В этом случае можно записать
становится равной нулю. В этом случае можно записать
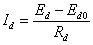 ,
,
где 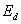 – среднее значение выпрямленного напряжения из регулировочной характеристики.
– среднее значение выпрямленного напряжения из регулировочной характеристики.
Пример. Рассчитать интервал проводимости 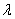 и среднее значение тока вентилей неуправляемого выпрямителя, выполненного по однофазной схеме со средней точкой и работающего на противо-ЭДС.
и среднее значение тока вентилей неуправляемого выпрямителя, выполненного по однофазной схеме со средней точкой и работающего на противо-ЭДС.
Исходные данные следующие:
действующее значение напряжение вторичной полуобмотки трансформатора 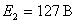 ;
;
противо-ЭДС в цепи постоянного тока 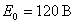 ;
;
внутреннее сопротивление источника противо-ЭДС 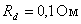 ;
;
индуктивность в цепи постоянного тока 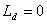 Ld=0.
Ld=0.
Определим по (11) угол отсечки вентилей 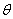 :
:
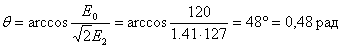 .
.
Тогда интервал проводимости вентилей
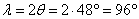 .
.
Среднее значение выпрямленного тока
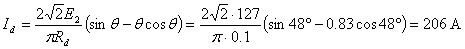 .
.
Среднее значение тока вентиля равно
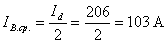 .
.
ЛИТЕРАТУРА
Архангельский Н.Л., Чистосердов В.Л. Системы управления электроприводами. Практ. пособие/ Иван. гос. энерг. ун-т. - Иваново, 2000. – 156 с.
Контрольные вопросы
1. На какие параметры схем выпрямления влияют коммутационные процессы?
2. От каких параметров схем выпрямления зависит падение напряжения в коммутационный период?
3. Что понимаем под внешней характеристикой, и какие параметры схемы влияют на ее характер?
4. Каким образом влияет противо-ЭДС нагрузки на параметры вентильного преобразователя?
5. В однофазной схеме рис.1 найти падение напряжения в коммутационный период, если известно, что 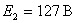 ,
, 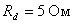 ,
, 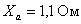 ,
, 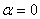 .
.
Ответ:
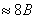
6. В однофазной мостовой схеме выпрямления найти падение напряжения и угол коммутации 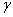 , если известно, что
, если известно, что 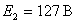 ,
, 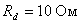 ,
, 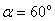 ,
, 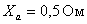 ,
, 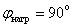 .
.
Ответ:
3.65 В, 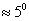 .
.
7. Найти напряжения внешней характеристики трехфазного мостового выпрямителя при холостом ходе и при нагрузке, если известно, что 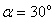 ,
, 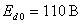 ,
, 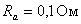 ,
, 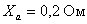 ,
, 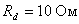 .
.
Ответ:
95 В, 90 В.